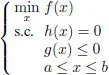Uncertainty and Optimization in Structural Mechanics

Abdelkhalak El Hami, Bouchaib Radi

• Publisher: Wiley-ISTE
• Year: 2013
• Print ISBN: 9781848215177
• eBook ISBN: 9781118711835
• Edition: 1
• Topic: Technology & Engineering
• Subtopic: Technology & Engineering Research & Skills
• Index: Technology & Engineering

Uncertainty and Optimization in Structural Mechanics

Optimization is generally a reduction operation of a definite quantity. This process naturally takes place in our environment and through our activities. For example, many natural systems evolve, in order to minimize their potential energy. Modeling these phenomena then largely relies on our capacity to artificially reproduce these processes. In parallel, optimization problems have quickly emerged from human activities, notably from economic concerns. This book includes the most recent ideas coming from research and industry in the field of optimization, reliability and the recognition of accompanying uncertainties. It is made up of eight chapters which look at the reviewing of uncertainty tools, system reliability, optimal design of structures and their optimization (of sizing, form, topology and multi-objectives) – along with their robustness and issues on optimal safety factors. Optimization reliability coupling will also be tackled in order to take into account the uncertainties in the modeling and resolution of the problems encountered. The book is aimed at students, lecturers, engineers, PhD students and researchers.

1

Uncertainty

In a large number of optimization problems, simulation software, coupled with an appropriate mathematical optimization algorithm, is used for problems such as finance [LID 04], transport [CAP 03], manufacturing [CHE 08] and biochemical engineering and design engineering, [GAN 02]. This approach has proven to be much more effective than standard trial and error procedures. This is, for the most part, due to the development of faster digital computers, more sophisticated calculation techniques and the combination of simulation software based on the finite element method and mathematical optimization techniques [MAK 98]. In the case of deterministic optimization, the design variable can be accurately controlled and has a specific value. The input and output of the optimization procedure will be determinist in this case.

1.1. Introduction

Integrating uncertainty into the design process is a practice commonly used by engineers. This concerns the design of systems for critical values, the use of safety factors, and the more advanced techniques from the calculation of reliability. The aim is to design a system with statistically better performance that may often change according to uncertainty. For example, we may want to obtain a level of performance which is minimally sensitive to uncertainty. We may also not want to surpass a minimal performance threshold with a given probability. In addition, design problems are still constrained optimization problems. Where there is uncertainty, we want to identify it with a high degree of probability.

This uncertainty is a naturally inherent characteristic that cannot be avoided. We can, for example, cite exterior load point clouds and environmental conditions, such as variations in temperature and material properties. Alongside controllable design variables, processes are influenced by noise or stochastic variables. This type of variable cannot be precisely ordered and has either an unknown or known distribution. In the latter case, the variable may be commonly expressed by an average value and a corresponding standard deviation [JAN 08]. The input variation then translates the responding quantity that attaches a distribution rather than a deterministic value.

With continual demands on manufacturers to improve quality, quality control plays an increasingly important role in industrial procedures. One method that uses statistical techniques to monitor and control product quality is termed statistic process control. The different demands generally include three main tasks in the following order:

– a control procedure;

– process diagnostics;

– taking corrective measures.

What does it take to adjust the uncertain process so that it is evaluated on the basis of knowledge of the system and the experience [WER 07]?

With movement toward an integrated computer manufacturing environment, the need to develop applications that allow the implementation of various statistical process control tasks must be automatic. The ability to predict the response of a forming metal process to change in the number of input parameters is crucial. This is because, very often, an obtained deterministic optimum is found at the crossover between one and several constraints. The natural variation in materials, due to lubrication and process parameters, which could lead to an increased number of constraint violations, results in a higher amount of scrap iron [STR 10]. To avoid this unwanted situation, uncertainty must be specifically accounted for in the optimization strategy to avoid faults in the product such as wrinkling and material fractures and faults in form.

An initial approach of accounting for uncertainty in optimization problems has been carried out by considering security factors. The factor must compensate for the variation in yield caused by uncertainty in the system. The greatest security factors correlate with the highest levels of uncertainty. In the majority of cases, these factors are derived on the basis of past experience, but this does not absolutely guarantee security or a satisfying level of performance [BEN 02].

In recent years, several approaches have been developed to explicitly account for uncertainty [BEY 07, PAR 06]. This is examined in a special issue of the Review of Computing Methods in Applied Mechanics [HUG 05] and several research projects [PAD 03]. In addition, several modules (or courses) have already combined statistical control techniques for processes with simulations of finite elements to quantify robustness, such as, for example, Autoform-Sigma and LS-Opt [CLE 10]. However, these packets are mainly concentrated around quantifying reliability and robustness in a given solution, rather than optimization under uncertainty. The deterministic optimization strategy is extended to take design variables into consideration. This approach allows the quantification and optimization of a process or design performance.

1.2. The optimization problem

The basic idea of optimization consists of minimizing an objective function, f, by finding the optimum value of one or several design variables x. In addition, several types of restrictions or constraints can be present as equality constraints h, inequality constraints g or a box of constraints. This last type of constraint is often defined as boundaries that identify the area in which design variables are authorized to vary according to an upper and lower limit. These boundaries are respectively indicated by a and b. In general, an optimization problem must be mathematically described as follows:

[1.1]

The solution to an optimization problem entails finding one of the optimum design values or the variables that minimize the objective functions subject to different constraints. This process requires an optimization algorithm for specific problem. The inequality and equality constraints can be divided into linear or nonlinear and explicit or implicit constraints. Explicit constraints depend directly on the design variables while implicit constraints depend indirectly on the design variables. In the latter case, an evaluation of the constraint function is required to evaluate whether or not the constraint is satisfactory.

The aim of an optimization procedure is to find an optimal design with a high degree of precision. Some critical factors concerning optimization procedures are as follows:

– The optimization procedure is carried out using models and/or approximations of reality. In the majority of cases, we do not know what the error in the model is. If this is the case, we cannot be certain that the optimum model is the true optimum. This indicates that the optimum solution, even if calculated very accurately, may be difficult to replicate in a real world application. Verification of the optimum model against the physical process is therefore highly recommended.

– If the aim of optimization is to improve product quality, it is also helpful to verify the economic feasibility of improving products. There is, in general, a compromise between a potentially more complex and costly manufacturing procedure and an increase in the new design’s performance. It is therefore recommended to favor an optimum economic product or tend rather towards the qualitative optimum.

– The following optimum design for an optimum procedure is a static optimum. However, it is, in reality, dynamic. For example, the process or environmental parameters may change over time and therefore the static optimum is only valid for a limited duration.

– Both the objective function and implicit constraints require an evaluation of the response since they inherently depend on the design variables. Each evaluation of the response is carried out by calculating the nonlinear finite elements, which is therefore costly in terms of calculation time.

– The evaluation of the response relating to the obtained optimum, a series of finite element simulations, must be carried out. As a result, an effective algorithm must reduce the number of these simulations.

– In particular, optimization procedures that incorporate uncertainty are significantly less time effective in relation to their deterministic counterparts. This is because the evaluation of the objective functions and constraints are more costly in uncertain conditions. It is therefore necessary to use an appropriate and effective technique to manage uncertainty in the optimization procedure.

– To limit the computational load when there is a combination of optimization strategies with finite element simulations, only a limited number of parameters may be studied. Other procedures which make the design problem less costly in terms of calculation include the use of approximation and parallel calculation [SCH 08].

– A final, crucial remark regarding digital simulation in the optimization process is that the latter may introduce new sources of point clouds, also known as digital noise [DES 08].

1.3. Sources of uncertainty

Optimization under uncertainty requires information regarding the uncertainty influencing the system. There are different sources of variation. Each type of uncertainty requires a different approach for use in the optimization procedure.

There are different scenarios where the designer has to deal with uncertainty. A metal forming the procedure or the product has an output or a response, f, that depen...

Table of contents

• Cover
• Contents
• Title Page
• Copyright Page
• Preface
• 1 Uncertainty
• 2 Reliability in Mechanical Systems
• 3 Optimal Structural Design
• 4 Multi-Object Optimization With Uncertainty
• 5 Robust Optimization
• 6 Reliability Optimization
• 7 Optimal Security Factors Approach
• 8 Reliability-Based Topology Optimization
• Bibliography
• Index