Color in Computer Vision

Fundamentals and Applications

Theo Gevers, Arjan Gijsenij, Joost van de Weijer, Jan-Mark Geusebroek

• Publisher: Wiley
• Year: 2012
• Print ISBN: 9780470890844
• eBook ISBN: 9781118350065
• Edition: 1
• Topic: Technology & Engineering
• Subtopic: Electrical Engineering & Telecommunications
• Index: Technology & Engineering

While the field of computer vision drives many of today's digital technologies and communication networks, the topic of color has emerged only recently in most computer vision applications. One of the most extensive works to date on color in computer vision, this book provides a complete set of tools for working with color in the field of image understanding.

Based on the authors' intense collaboration for more than a decade and drawing on the latest thinking in the field of computer science, the book integrates topics from color science and computer vision, clearly linking theories, techniques, machine learning, and applications. The fundamental basics, sample applications, and downloadable versions of the software and data sets are also included. Clear, thorough, and practical, Color in Computer Vision explains:

• Computer vision, including color-driven algorithms and quantitative results of various state-of-the-art methods
• Color science topics such as color systems, color reflection mechanisms, color invariance, and color constancy
• Digital image processing, including edge detection, feature extraction, image segmentation, and image transformations
• Signal processing techniques for the development of both image processing and machine learning
• Robotics and artificial intelligence, including such topics as supervised learning and classifiers for object and scene categorization Researchers and professionals in computer science, computer vision, color science, electrical engineering, and signal processing will learn how to implement color in computer vision applications and gain insight into future developments in this dynamic and expanding field.

Chapter 1: Introduction

Color is one of the most important and fascinating aspects of the world surrounding us. To comprehend the broad characteristics of color, a range of research fields has been actively involved, including physics (light and reflectance modeling), biology (visual system), physiology (perception), linguistics (cultural meaning of color), and art.

From a historical perspective, covering more than 400 years, prominent researchers contributed to our present understanding of light and color. Snell and Descartes (1620–1630) formulated the law of light refraction. Newton (1666) discovered various theories on light spectrum, colors, and optics. The perception of color and the influence on humans has been studied by Goethe in his famous book “Farbenlehre” (1840). Young and Helmholtz (1850) proposed the trichromatic theory of color vision. Work on light and color resulted in quantum mechanics elaborated by Max Planck, Albert Einstein, and Niels Bohr. In art (industrial design), Albert Munsell (1905) invented the theory on color ordering in his “A Color Notation.” Further, the value of the biological and therapeutic effects of light and color have been analyzed, and views on color from folklore, philosophy, and language have been articulated by Schopenhauer, Hegel, and Wittgenstein.

Over the last decades, with the technological advances of printers, displays, and digital cameras, an explosive growth in the diversity of needs in the field of color computer vision has been witnessed. More and more, the traditional gray value imaginary is replaced by color systems. Moreover, today, with the growth and popularity of the World Wide Web, a tremendous amount of visual information, such as images and videos, has become available. Hence, nowadays, all visual data is available in color. Furthermore, (automatic) image understanding is becoming indispensable to handle large amount of visual data. Computer vision deals with image understanding and search technology for the management of large-scale pictorial datasets. However, in computer vision, the use of color has been only partly explored so far.

This book determines the use of color in computer vision. We take on the challenge of providing a substantial set of color theories, computational methods, and representations, as well as data structures for image understanding in the field of computer vision. Invariant and color constant feature sets are presented. Computational methods are given for image analysis, segmentation, and object recognition. The feature sets are analyzed with respect to their robustness to noise (e.g., camera noise, occlusion, fragmentation, and color trustworthiness), expressiveness, discriminative power, and compactness (efficiency) to allow for fast visual understanding. The focus is on deriving semantically rich color indices for image understanding. Theoretical models are presented to express semantics from both a physical and a perceptual point of view.

1.1 From Fundamental to Applied

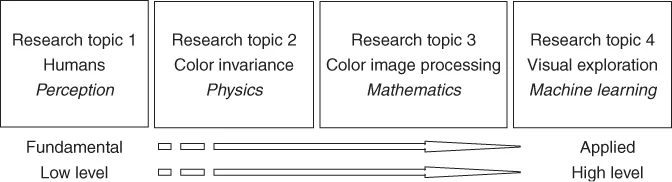
The aim of this book is to present color theories and techniques for image understanding from (low level) basic color image formation to (intermediate level) color invariant feature extraction and color image processing to (high level) learning of object and scene recognition by semantic detectors. The topics, and corresponding chapters, are organized from low level to high level processing and from fundamental to more applied research. Moreover, each topic is driven by a different research area using color as an important stand-alone research topic and as a valuable collaborative source of information bridging the gap between different research fields (Fig. 1.1).

Figure 1.1 The different topics are organized from low level to high level processing and from fundamental to more applied research. Each topic is driven by a different research area from human perception, physics, and mathematics to machine learning.

The book starts with the explanation of the mechanisms of human color perception. Understanding the human visual pathway is crucial for computer vision systems, which aim to describe color information in such a way that it is relevant to humans.

Then, physical aspects of color are studied, resulting in reflection models from which photometric invariance is derived. Photometric invariance is important for computer vision, as it results in color measurements that are independent of accidental imaging conditions such as a change in camera viewpoint or a variation in the illumination.

A mathematical perspective is taken to cope with the difference between gray value (scalar) and color (vector) information processing, that is, the extension of single-channel signal to multichannel signal processing. This mathematical approach will result in a sound way to perform color processing to obtain (low level) computational methods for (local) feature computation (e.g., color derivatives), descriptors (e.g., SIFT), and image segmentation. Furthermore, based on both mathematical and physical fundamentals, color image feature extraction is presented by integrating differential operators and color invariance.

Finally, color is studied in the context of machine learning. Important topics are color constancy, photometric invariance by learning, and color naming in the context of object recognition and video retrieval. On the basis of the multichannel approach and color invariants, computational methods are presented to extract salient image patches. From these salient image patches, color descriptors are computed. These descriptors are used as input for various machine learning methods for object recognition and image classification.

The book consists of five parts, which are discussed next.

1.2 Part I: Color Fundamentals

The observed color of an object depends on a complex set of imaging conditions. Because of the similarity in trichromatic color processing between humans and computer vision systems, in Chapter 2, an outline on human color vision is provided. The different stages of color information processing along the human visual pathway are presented. Further, important chromatic properties of the visual system are discussed such as chromatic adaptation and color constancy. Then, to provide insights in the imaging process, in Chapter 3, the basics on color image formation are presented. Reflection models are introduced describing the imaging process and how photometric changes, such as shadows and specularities, influence the RGB values in an image. Additionally, a set of relevant color spaces are enumerated.

1.3 Part II: Photometric Invariance

In computer vision, invariant descriptions for image understanding are relatively new but quickly gaining ground. The aim of photometric invariant features is to compute image properties of objects irrespective of their recording conditions. This comes, in general, at the loss of some discriminative power. To arrive at invariant features, the imaging process should be taken into account.

In Chapters 4–6, the aim is to extract color invariant information derived from the physical nature of objects in color images using reflection models. Reflection models are presented to model dull and gloss materials, as well as shadows, shading, and specularities. In this way, object characteristics can be derived (based on color/texture statistics) for the purpose of image understanding. Physical aspects are investigated to model and analyze object characteristics (color and texture) under different viewing and illumination conditions. The degree of invariance should be tailored to the recording circumstances. In general, a color model with a very wide class of invariance loses the power to discriminate among object differences. Therefore, in Chapter 6, the aim is to select the tightest set of invariants suited for the expected set of nonconstant conditions.

1.3.1 Invariance Based on Physical Properties

As discussed in Chapter 4, most of the methods to derive photometric invariance are using 0th order photometric information, that is, pixel values. The effect of the reflection models on higher-order- or differential-based algorithms remained unexplored for a long time. The drawbacks of the photometric invariant theory (i.e., the loss of discriminative power and deterioration of noise characteristics) are inherited by the differential operations. To improve the performance of differential-based algorithms, the stability of photometric invariants can be increased through the noise propagation analysis of the invariants. In Chapters 5 and 6, an overview is given on how to advance the computation of both photometric invariance and differential information in a principled way.

1.3.2 Invariance By Machine Learning

While physical-based reflection models are valid for many different materials, it is often difficult to model the reflection of complex materials (e.g., with nonperfect Lambertian or dielectrical surfaces) such as human skin, cars, and road decks. Therefore, in Chapter 7, we also present techniques to estimate photometric invariance by machine learning models. On the basis of these models, computational methods are studied to derive the (in)sensitivity of transformed color channels to photometric effects obtained from a set of training samples.

1.4 Part III: Color Constancy

Differences in illumination cause measurements of object colors to be biased toward the color of the light source. Humans have the ability of color constancy; they tend to perceive stable object colors despite large differences in illumination. A similar color constancy capability is necessary for various computer vision applications such as image segmentation, object recognition, and scene classification.

In Chapters 8–10, an overview is given on computational color constancy. Many state-of-the-art methods are tested on different (freely) available datasets. As color constancy is an underconstrained problem, color constancy algorithms are based on specific imaging assumptions. These assumptions include the set of possible light sources, the spatial and spectral characteristics of scenes, or other assumptions (e.g., the presence of a white patch in the image or that the averaged color is gray). As a consequence, no algorithm can be considered as universal. With the large variety of available methods, the inevitable question, that is, how to select the method that induces the equivalence class for a certain imaging setting, arises. Furthermore, the subsequent question is how to combine the different algorithms in a proper way. In Chapter 11, the problem of how to select and combine different methods is addressed. An evaluation of color constancy methods is given in Chapter 12.

1.5 Part IV: Color Feature Extraction

We present how to extend luminance-based algorithms to the color domain. One requirement is that image processing methods do not introduce new chromaticities. A second implication is that for differential-based algorithms, the derivatives of the separate channels should be combined without loss of derivative information. Therefore, the implications on the multichannel theory are investigated, and algorithmic extensions for luminance-based feature detectors such as edge, curvature, and circular detectors are given. Finally, the photometric invariance theory described in earlier parts of the book is applied to feature extraction.

1.5.1 From Luminance to Color

The aim is to take an algebraic (vector based) approach to extend scalar-signal to vector-signal processing. However, a vector-based approach is accompanied by several mathematical obstacles. Simply applying existing luminance-based operators on the separate color channels, and subsequently combining them, will fail because of undesired artifacts.

As a solution to the opposing vector problem, for the computation of the color gradient, the color tensor (structure tensor) is presented. In Chapter 13, we give a review on color-tensor-based techniques on how to combine derivatives to compute local structures in color images in a principled way. Adaptations of the tensor lead to a variety of local image features, such as circle detectors, curvature estimation, and optical flow.

1.5.2 Features, Descriptors, and Saliency

Although color is important to express saliency, the explicit incorporation of color distinctiveness into the design of image feature detectors has been largely ignored. To this end, we give an overview on how color distinctiveness can be explicitly incorporated in the design of color (invariant) representations and feature detectors. The approach is based on the analysis of the statistics of color derivatives. Furthermore, we present color descriptors for the purpose of object recognition. Object recogniti...

Table of contents

• Cover
• Copyright
• Series
• Title Page
• Preface
• Chapter 1: Introduction
• Part I: Color Fundamentals
• Part II: Photometric Invariance
• Part III: Color Constancy
• Part IV: Color Feature Extraction
• Part V: Applications
• Citation Guidelines
• References
• Index