Remote Sensing Imagery

Florence Tupin, Jordi Inglada, Jean-Marie Nicolas, Florence Tupin, Jordi Inglada, Jean-Marie Nicolas

• Publisher: Wiley-ISTE
• Year: 2014
• Print ISBN: 9781848215085
• eBook ISBN: 9781118898925
• Edition: 1
• Topic: Technology & Engineering
• Subtopic: Civil Engineering
• Index: Technology & Engineering

Dedicated to remote sensing images, from their acquisition to their use in various applications, this book covers the global lifecycle of images, including sensors and acquisition systems, applications such as movement monitoring or data assimilation, and image and data processing.
It is organized in three main parts. The first part presents technological information about remote sensing (choice of satellite orbit and sensors) and elements of physics related to sensing (optics and microwave propagation). The second part presents image processing algorithms and their specificities for radar or optical, multi and hyper-spectral images. The final part is devoted to applications: change detection and analysis of time series, elevation measurement, displacement measurement and data assimilation.
Offering a comprehensive survey of the domain of remote sensing imagery with a multi-disciplinary approach, this book is suitable for graduate students and engineers, with backgrounds either in computer science and applied math (signal and image processing) or geo-physics.

About the Authors

Florence Tupin is Professor at Telecom ParisTech, France. Her research interests include remote sensing imagery, image analysis and interpretation, three-dimensional reconstruction, and synthetic aperture radar, especially for urban remote sensing applications.
Jordi Inglada works at the Centre National d'Études Spatiales (French Space Agency), Toulouse, France, in the field of remote sensing image processing at the CESBIO laboratory. He is in charge of the development of image processing algorithms for the operational exploitation of Earth observation images, mainly in the field of multi-temporal image analysis for land use and cover change.
Jean-Marie Nicolas is Professor at Telecom ParisTech in the Signal and Imaging department. His research interests include the modeling and processing of synthetic aperture radar images.

Part 1

Systems, Sensors and Acquisitions

Chapter 1

Systems and Constraints

1.1. Satellite systems

A remote sensing satellite placed in orbit around the Earth is subject to several gravitational forces that will define its trajectory and motion. We will see that orbit formalism dates as far as Kepler (1609), and the motion of satellites is modeled using Newton’s laws. The Earth has specific properties, such as being flat at the poles; these specificities will introduce several changes to the Kepler model: quite strangely, as we will see, the consequences will turn out be extremely beneficial for remote sensing satellites, since they will allow us to have heliosynchronous sensors; this will enable them to acquire data at the same time as the solar hour, which in turn simplifies the comparisons of the respective data acquisitions.

The objective of this chapter is to briefly analyze orbital characteristics in order to draw some conclusions regarding the characteristics of imaging systems that orbit the Earth. For more details, readers can refer to the work of Capderou [CAP 03].

1.2. Kepler’s and Newton’s laws

By studying the appearance of the planets around the Sun (and, in particular, that of Mars), in 1609, Kepler proposed (in a purely phenomenological manner) the following three laws describing the motion of planets around the Sun:

– The planets’ trajectory lies in a plane and is represented by an ellipse having the Sun as its focus.

– The area swept out by the segment joining the Sun and the planet during a given period of time is constant.

– The square of the revolution period is proportional to the cube of the length of the major axis of the ellipse.

In 1687, Newton demonstrated these laws by giving us a model of the universal attraction. This model stipulates that two punctual masses m and M exercise a force F against each other, colinear to the line joining these two masses:

with G = 6.672 × 10^–11 being the gravitational constant. Therefore, an interaction takes place between the two masses.

In the case of artificial satellites orbiting the Earth, it is obvious that the Earth’s mass (M_T = 5.5974 × 10²⁴ kg) is extremely large with respect to the mass of the satellite and we can easily assume that the center of the Earth may be mingled with the gravitational center of the Earth + satellite system. If we also assume that the Earth is a homogeneous sphere, we can consider it as a punctual mass by applying the Gauss theorem. The satellite with a mass m, located at a distance r from the Earth (with a mass M_T), is then subjected to a so-called attractive “central force”:

with μ = G M_T = 3.986 × 10¹⁴ m³s ^–2. Therefore, we can say that we have a central potential U (r):

[1.1]

This force being the only one that can modify the motion of the satellite, we can therefore show that this motion verifies the following essential properties:

– The trajectory of the satellite lies in a plane, the “orbital plane”. The distance r verifies, using polar coordinates, the equation of an ellipse:

[1.2]

described by two parameters: the eccentricity e and the parameter p of the ellipse. The Earth is at one of the foci of this ellipse: this is the first Kepler law. For an ellipse, a trajectory point is solely determined by the angle θ. Just like for θ′ = θ + 2π we find the same position values, we can say that the trajectory is closed in the orbital plane. The period of time that a satellite needs to pass from an angle θ to an angle θ + 2π is called a period: this is the period of time required for circling the Earth. An elliptic orbit has two main points:

– for θ – θ₀ = 0, we see that value r is at its minimum. We say that we are at the “perigee”: the distance to Earth is denoted as r_P;

– for θ – θ₀ = π, we see that the value r is at its maximum. We say that we are at the “apogee”: the distance to Earth is denoted as r_A.

We can easily deduce the relations:

[1.3]

– Since the attractive force is colinear to the distance vector

, and there is no other force, the angular momentum

[1.4]

is conserved, so that:

where C is a constant that represents the law of equal areas, i.e. the second Kepler law.

– An ellipse can be characterized by its semimajor axis a defined by:

By applying the law of equal areas, we obtain the period T of the satellite:

[1.5]

which is the expression of the third Kepler law. The parameters of this period T are, therefore, only a – the semimajor axis – and μ (related to the Earth’s mass).

On an ellipse, the speed is not constant. We show that

[1.6]

except when we have a perfectly circular trajectory, for which we have:

[1.7]

The speed of a satellite varies along its trajectory around the Earth. The speed is, therefore, higher as the distance r becomes smaller. More specifically, if v_P is the speed at the perigee (with r_P = a(1 – e)) and v_A is the speed at the apogee (with r_A = a(1 + e)), we get:

From this, we may then deduce the following useful relation:

[1.8]

which shows that the ratio of the speeds to the perigee and apogee depends only on the eccentricity and therefore on the shape of the ellipse.

To conclude on the general aspects of orbits, we must emphasize the fact that these ellipses only need two parameters to be described accurately. We often choose a, the semimajor axis, and e, the eccentricity.

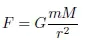
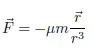
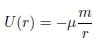
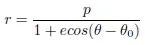
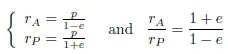
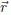
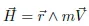
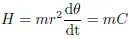
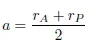
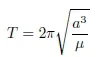
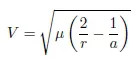
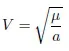
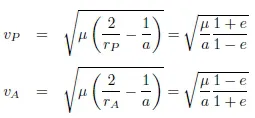
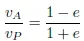
1.3. The quasi-circular orbits of remote sensing satellites

The satellite era started with the launch of the first satellite Sputnik in 1957. Some numbers of civilian remote sensing satellites have since been placed in orbit around the Earth. These orbits, whose eccentricity is very low (e < 0.001), are quasi-circular and, therefore, described either by the semimajor axis a or by their altitude h, defined by the relation:

with R_T = 6, 378.137 km being the radius of the Earth at the equator. We often speak of a circular orbit for this type of orbit.

Choosing an orbit for a remote sensing satellite needs to consider several things. First and foremost, since we can show that the energy of an orbit only depends on the semimajor axis a, we must note that the choice in altitude is restrictive in terms of launch: a high altitude requires a launcher that is both heavy and expensive. Therefore, it does not seem to be appropriate to choose a high altitude for an optical imaging system: the resolution being proportional to the distance, a low altitude will allow u...

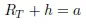
Table of contents

• Cover Page
• Contents
• Title Page
• Copyright
• Preface
• Part 1: Systems, Sensors and Acquisitions
• Part 2: Physics and Data Processing
• Part 3: Applications: Measures, Extraction, Combination and Information Fusion
• Bibliography
• List of Authors
• Index