Practical Multiscaling

Jacob Fish

• Publisher: Wiley
• Year: 2013
• Print ISBN: 9781118410684
• eBook ISBN: 9781118534854
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Mechanics

Practical Multiscaling covers fundamental modelling techniques aimed at bridging diverse temporal and spatial scales ranging from the atomic level to a full-scale product level. It focuses on practical multiscale methods that account for fine-scale (material) details but do not require their precise resolution. The text material evolved from over 20 years of teaching experience at Rensselaer and Columbia University, as well as from practical experience gained in the application of multiscale software.

This book comprehensively covers theory and implementation, providing a detailed exposition of the state-of-the-art multiscale theories and their insertion into conventional (single-scale) finite element code architecture. The robustness and design aspects of multiscale methods are also emphasised, which is accomplished via four building blocks: upscaling of information, systematic reduction of information, characterization of information utilizing experimental data, and material optimization. To ensure the reader gains hands-on experience, a companion website hosting a lite version of the multiscale design software (MDS-Lite) is available.

Key features:

• Combines fundamental theory and practical methods of multiscale modelling
• Covers the state-of-the-art multiscale theories and examines their practical usability in design
• Covers applications of multiscale methods
• Accompanied by a continuously updated website hosting the multiscale design software
• Illustrated with colour images

Practical Multiscaling is an ideal textbook for graduate students studying multiscale science and engineering. It is also a must-have reference for government laboratories, researchers and practitioners in civil, aerospace, pharmaceutical, electronics, and automotive industries, and commercial software vendors.

1

Introduction to Multiscale Methods

1.1 The Rationale for Multiscale Computations

Consider a textbook boundary value problem that consists of equilibrium, kinematical, and constitutive equations together with essential and natural boundary conditions. These equations can be classified into two categories: those that directly follow from physical laws and those that do not. A constitutive equation demonstrates a relation between two physical quantities that is specific to a material or substance and does not follow directly from physical laws. It can be combined with other equations (equilibrium and kinematical equations, which do ­represent physical laws) to solve specific physical problems.

In other words, it is convenient to label all that we do not know about the boundary value problem as a constitutive law (a term originally coined by Walter Noll in 1954) and designate an experimentalist to quantify the constitutive law parameters. While this is a trivial exercise for linear elastic materials, this is not the case for anisotropic history-dependent materials well into their nonlinear regime. In theory, if a material response is history-dependent, an infinite number of experiments would be needed to quantify its response. In practice, however, a handful of constitutive law parameters are believed to “capture” the various failure mechanisms that have been observed experimentally. This is known as phenomenological modeling, which relates several different empirical observations of phenomena to each other in a way that is consistent with fundamental theory but is not directly derived from it.

An alternative to phenomenological modeling is to derive constitutive equations (or directly, field quantities) from finer scale(s) where established laws of physics are believed to be better understood. The enormous gains that can be accrued by this so-called multiscale approach have been reported in numerous articles [1,2,3,4,5,6]. Multiscale computations have been identified (see page 14 in [7]) as one of the areas critical to future nanotechnology advances. For example, the FY2004 US$3.7 billion National Nanotechnology Bill (page 14 in [7]) states that “approaches that integrate more than one such technique (…molecular ­simulations, continuum-based models, etc.) will play an important role in this effort.”

Figure 1.1 Reduced precision due to increase in uncertainty and/or complexity. CMC, ceramic matrix composite; MMC, metal matrix composite

One of the main barriers to such a multiscale approach is the increased uncertainty and complexity introduced by finer scales, as illustrated in Figure 1.1. As a guiding principle for assessing the need for finer scales, it is appropriate to recall Einstein’s statement that “the model used should be the simplest one possible, but not simpler.” The use of any multiscale approach has to be carefully weighed on a case-by-case basis. For example, in the case of metal matrix composites (MMCs) with an almost periodic arrangement of fibers, introducing finer scales might be advantageous since the bulk material typically does not follow normality rules, and developing a phenomenological coarse-scale constitutive model might be challenging at best. The behavior of each phase is well understood, and obtaining the overall response of the material from its fine-scale constituents can be obtained using homogenization. On the other hand, in brittle ceramic matrix composites (CMCs), the microcracks are often randomly distributed and characterization of their interface properties is difficult. In this case, the use of a multiscale approach may not be the best choice.

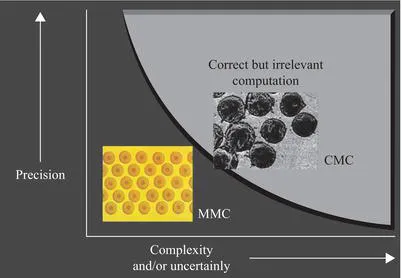
1.2 The Hype and the Reality

Multiscale Science and Engineering is a relatively new field [8,9] and, as with most new technologies, began with a naive euphoria (Figure 1.2). During the euphoria stage of technology development, inventors can become immersed in the ideas themselves and may overpromise, in part to generate funds to continue their work. Hype is a natural handmaiden to overpromise, and most technologies build rapidly to a peak of hype [10].

For instance, early success in expert systems led to inflated claims and unrealistic expectations. The field did not grow as rapidly as investors had been led to expect, and this translated into disillusionment. In 1981 Feigenbaum et al. [11] reckoned that although artificial intelligence (AI) was already 25 years old, it “was a gangly and arrogant youth, yearning for a maturity that was nowhere evident.” Interestingly, today you can purchase the hardcover AI handbook [11] for as little as US$0.73 on Amazon. Multiscale ­computations also had their share of overpromise, such as inflated claims of designing drugs atom by atom [12] or reliably designing the Boeing 787 from first principles, just to mention a few.

Figure 1.2 Evolution of new technology

Following this naive euphoria (Figure 1.2), there is almost always an overreaction to ideas that are not fully developed, and this inevitably leads to a crash, followed by a period of ­wallowing in the depths of cynicism. Many new technologies evolve to this point and then fade away. The ones that survive do so because industry (or perhaps someone else) finds a “good use” (a true user benefit) for this new technology.

The author of this book believes that the state of the art today in multiscale science and engineering is sufficiently mature to take on the more than 50-year-old challenge [13] posed by Nobel Prize Laureate Richard Feynman: “What would the properties of materials be if we could really arrange the atoms the way we want them?” However, progress toward fulfilling the promise of multiscale science and engineering hinges not only on its development as a discipline concerned with the understanding and integration of mathematical, computational, and domain expertise sciences, but more so with its ability to meet broader societal needs beyond those of interest to the academic community. After all, as compelling as a finite element theory is, the future of that field might have been in doubt if practitioners had not embraced it.

Thus, the primary o...

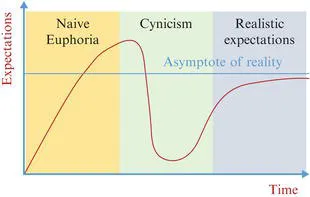
Table of contents

• Cover
• Title page
• Copyright page
• Dedication
• Preface
• Acknowledgments
• 1 Introduction to Multiscale Methods
• 2 Upscaling/Downscaling of Continua
• 3 Upscaling/Downscaling of Atomistic/Continuum Media
• 4 Reduced Order Homogenization
• 5 Scale-separation-free Upscaling/Downscaling of Continua
• 6 Multiscale Design Software
• Index