Introductory Modern Algebra

A Historical Approach

Saul Stahl

• Publisher: Wiley
• Year: 2013
• Print ISBN: 9780470876169
• eBook ISBN: 9781118552032
• Edition: 2
• Topic: Mathematik
• Subtopic: Weltgeschichte

Praise for the First Edition

"Stahl offers the solvability of equations from the historical point of view...one of the best books available to support a one-semester introduction to abstract algebra."
—CHOICE

Introductory Modern Algebra: A Historical Approach, Second Edition presents the evolution of algebra and provides readers with the opportunity to view modern algebra as a consistent movement from concrete problems to abstract principles. With a few pertinent excerpts from the writings of some of the greatest mathematicians, the Second Edition uniquely facilitates the understanding of pivotal algebraic ideas.

The author provides a clear, precise, and accessible introduction to modern algebra and also helps to develop a more immediate and well-grounded understanding of how equations lead to permutation groups and what those groups can inform us about such diverse items as multivariate functions and the 15-puzzle. Featuring new sections on topics such as group homomorphisms, the RSA algorithm, complex conjugation, the factorization of real polynomials, and the fundamental theorem of algebra, the Second Edition also includes:

• An in-depth explanation of the principles and practices of modern algebra in terms of the historical development from the Renaissance solution of the cubic equation to Dedekind's ideals
• Historical discussions integrated with the development of modern and abstract algebra in addition to many new explicit statements of theorems, definitions, and terminology
• A new appendix on logic and proofs, sets, functions, and equivalence relations
• Over 1,000 new examples and multi-level exercises at the end of each section and chapter as well as updated chapter summaries

Introductory Modern Algebra: A Historical Approach, Second Edition is an excellent textbook for upper-undergraduate courses in modern and abstract algebra.

Chapter 1

THE EARLY HISTORY

THIS CHAPTER CONTAINS an informal account of the early history of the issue of solvability of equations of degrees one, two, and three in a single unknown. The formulas that provide the solutions lead in a natural way to the discussion of the origins of complex numbers. We also take this opportunity to review some well-known information about the quadratic equation.

1.1 The Breakthrough

There is a general agreement among historians of mathematics that modern mathematics came into being in the mid sixteenth century when the combined efforts of the Italian mathematicians Scipione del Ferro, Niccolò Tartaglia, and Gerolamo Cardano produced a formula for the solution of cubic equations. For the first time ever west European mathematicians succeeded in cracking a problem whose solution eluded the best mathematical minds of antiquity. Archimedes, one of the greatest mathematicians, scientists, and engineers of all times, had solved some cubic equations in terms of the intersections of a suitable parabola and hyperbola. Omar Khayyam, one of the most prominent of the Arab mathematicians and poets, also expended much effort on his geometrical solutions of special cases of the cubic equation but could not find the general formula. However, the significance of this accomplishment of the Renaissance mathematicians is not limited to the difficulty of the problem that was solved. We shall try to show how the issues raised by this solution eventually led to the creation of modern algebra and the discovery of mathematical landscapes that were undreamt of, even by such imaginative investigators as Archimedes and Khayyam.

The interest in algebraic equations goes back to the beginnings of written history. The Rhind Mathematical Papyrus, found in Egypt circa 1856 is a copy of a list of mathematical problems compiled some time during the second half of the nineteenth century BCE, or possibly even earlier. The twenty-fourth of these problems reads: “A quantity and its 1/7 added become 19. What is the quantity?” In other words, what is the solution to the equation

The method employed by the scribe has come to be known as the method of false position. He replaces the unknown by 7 and observes that

From this he concludes that the correct answer is obtained upon multiplying the first guess of 7 by 19/8:

Interestingly enough, the scribe does double check his solution by substituting it into the original problem and verifying that

We will not discuss the merits and limitations of the method of false position except to note that the idea of obtaining a correct solution to an equation by starting out with a possibly false guess and then modifying that guess has been refined into powerful techniques for finding numerical solutions, one of which will be described in Section 3.3. We do, however, wish to point out that the general first-degree equation is today defined as

and that the rules of algebra yield

as its unique solution.

The Mesopotamian mathematicians of that time could solve much more intricate equations, and had in fact already developed techniques for solving what we nowadays call quadratic equations. These techniques employed the geometrical method of “completing the square.” The Greeks, Indians, and Arabs all were aware of this method, having either derived them independently or perhaps learnt them from their predecessors and/or neighbors. In the ninth century the Persian mathematician al-Khwarizmi

wrote the book Hisab al-jabr w’al-muqa-balah

in which he carefully explained a compendium of algebraic techniques learnt from several past civilizations. The clarity of his exposition won both him and his book immortality in that the portion al-jabr of the title evolved into the word algebra, and the author’s name is the source of the word algorithm. An excerpt from this book expounding the solution to the quadratic equation

appears in Appendix A. The modern solution of the quadratic also relies on the completion of the square. The general quadratic equation has the f...

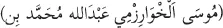
Table of contents

• Cover
• Half Title page
• Title page
• Copyright page
• Preface
• Chapter 1: The Early History
• Chapter 2: Complex Numbers
• Chapter 3: Solutions of Equations
• Chapter 4: Modular Arithmetic
• Chapter 5: The Binomial Theorem and Modular Powers
• Chapter 6: Polynomials Over A Field
• Chapter 7: Galois Fields
• Chapter 8: Permutations
• Chapter 9: Groups
• Chapter 10: Quotient Groups and Their Uses
• Chapter 11: Topics in Elementary Group Theory
• Chapter 12: Number Theory
• Chapter 13: The Arithmetic of Ideals
• Chapter 14: Abstract Rings
• A. Excerpts from Al-Khwarizmi’s Solution of the Quadratic Equation1
• B. Excerpts from Cardano’s Ars Magna1
• C. Excerpts from Abel’s A Demonstration of the Impossibility of the Algebraic Resolution of General Equations Whose Degree Exceeds Four1
• D. Excerpts from Galois’s On the Theory of Numbers1
• E. Excerpts from Cayley’s The Theory of Groups1
• F. Mathematical Induction
• G. Logic, Predicates, Sets, and Functions
• Biographies
• Bibliography
• Solutions to Selected Exercises
• Index
• Notation