Statistical Hypothesis Testing with SAS and R

Dirk Taeger, Sonja Kuhnt

• Publisher: Wiley
• Year: 2014
• Print ISBN: 9781119950219
• eBook ISBN: 9781118762615
• Edition: 1
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

A comprehensive guide to statistical hypothesis testing with examples in SAS and R

When analyzing datasets the following questions often arise:

Is there a short hand procedure for a statistical test available in SAS or R?
If so, how do I use it?
If not, how do I program the test myself?

This book answers these questions and provides an overview of the most common
statistical test problems in a comprehensive way, making it easy to find and perform
an appropriate statistical test.

A general summary of statistical test theory is presented, along with a basic
description for each test, including the necessary prerequisites, assumptions, the
formal test problem and the test statistic. Examples in both SAS and R are provided,
along with program code to perform the test, resulting output and remarks
explaining the necessary program parameters.

Key features:
• Provides examples in both SAS and R for each test presented.
• Looks at the most common statistical tests, displayed in a clear and easy to follow way.
• Supported by a supplementary website http://www.d-taeger.de featuring example
program code.

Academics, practitioners and SAS and R programmers will find this book a valuable
resource. Students using SAS and R will also find it an excellent choice for reference
and data analysis.

Part I

Introduction

The theory of statistical hypothesis testing was basically founded one hundred years ago by the Britons Ronald Aylmer Fisher, Egon Sharpe Pearson, and the Pole Jerzy Neyman. Nowadays it seems that we have a unique test theory for testing statistical hypothesis, but the opposite is true. On one hand Fisher developed the theory of significance testing and on the other hand Neyman and Pearson the theory of hypothesis testing.

Whereas with the Fisher theory the formulation of a null hypothesis is enough, Neyman's and Pearson's theory demands alternative hypotheses as well. They open the door to calculating error probabilities of two kinds, namely of a false rejection (type I error) and of a false acceptance (type II error) of the null hypothesis. This leads to the well known Neyman–Pearson lemma which helps us to find the best critical region for a hypothesis test with a simple alternative. The largest difference of both schools, however, are the Fisherian measure of evidence (p-value) and the Neyman–Pearson error rate (

).

With the Neyman–Pearson theory the error rate

is fixed and must be defined before performing the test. Within the Fisherian context the p-value is calculated from the value of the test statistic as a quantile of the test statistic distribution and serves as a measure of disproving the null hypothesis. Over the decades both theories have merged together. Today it is common practice – and described by most textbooks – to perform a Neyman–Pearson test and, instead of comparing the value of the test statistic with the critical region, to decide from the p-value. As this book is on testing statistical hypothesis with SAS and R we follow the common approach of mixing both theories. In SAS and R the critical regions are not reported, only p-values are given. We want to make the reader aware of this situation. In the next two chapters we shortly summarize the concept of statistical hypothesis testing and introduce the performance of statistical tests with SAS and R.

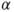
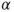
Chapter 1

Statistical hypothesis testing

1.1 Theory of statistical hypothesis testing

Hypothesis testing is a key tool in statistical inference next to point estimation and confidence sets. All three concepts make an inference about a population based on a sample taken from it. Hypothesis testing aims at a decision on whether or not a hypothesis on the nature of the population is supported by the sample.

In the following we shortly run through the steps of a statistical test procedure and introduce the notation used throughout this book. For a detailed mathematical explanation please refer to the book by Lehmann (1997).

We denote a sample of size

by

, where the

are observations of identically independently distributed random variables

,

. Usually some further assumptions are needed concerning the nature of the mechanism generating the sample. These can be rather general assumptions like a symmetric continuous distribution. Often a parametric distribution is assumed with only parameter values unknown, for example, the Gaussian distribution with both or either unknown mean and variance. In this ca...

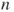
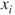
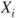
Table of contents

• Cover
• Title Page
• Copyright
• Dedication
• Preface
• Part I: Introduction
• Part II: Normal Distribution
• Part III: Binomial Distribution
• Part IV: Other Distributions
• Part V: Correlation
• Part VI: Nonparametric Tests
• Part VII: Goodness-of-Fit Tests
• Part VIII: Tests on Randomness
• Part IX: Tests on Contingency Tables
• Part X: Tests on Outliers
• Part XI: Tests in Regression Analysis
• Appendix A: Datasets
• Appendix B: Tables
• Glossary
• Index