Probability

With Applications and R

Robert P. Dobrow

• Publisher: Wiley
• Year: 2013
• Print ISBN: 9781118241257
• eBook ISBN: 9781118589441
• Edition: 1
• Topic: Matematica
• Subtopic: Matematica generale

An introduction to probability at the undergraduate level

Chance and randomness are encountered on a daily basis. Authored by a highly qualified professor in the field, Probability: With Applications and R delves into the theories and applications essential to obtaining a thorough understanding of probability.

With real-life examples and thoughtful exercises from fields as diverse as biology, computer science, cryptology, ecology, public health, and sports, the book is accessible for a variety of readers. The book's emphasis on simulation through the use of the popular R software language clarifies and illustrates key computational and theoretical results.

Probability: With Applications and R helps readers develop problem-solving skills and delivers an appropriate mix of theory and application. The book includes:

• Chapters covering first principles, conditional probability, independent trials, random variables, discrete distributions, continuous probability, continuous distributions, conditional distribution, and limits
• An early introduction to random variables and Monte Carlo simulation and an emphasis on conditional probability, conditioning, and developing probabilistic intuition
• An R tutorial with example script files
• Many classic and historical problems of probability as well as nontraditional material, such as Benford's law, power-law distributions, and Bayesian statistics
• A topics section with suitable material for projects and explorations, such as random walk on graphs, Markov chains, and Markov chain Monte Carlo
• Chapter-by-chapter summaries and hundreds of practical exercises

Probability: With Applications and R is an ideal text for a beginning course in probability at the undergraduate level.

1

FIRST PRINCIPLES

First principles, Clarice. Read Marcus Aurelius. Of each particular thing ask: what is it in itself? What is its nature?

—Hannibal Lecter, Silence of the Lambs

1.1 RANDOM EXPERIMENT, SAMPLE SPACE, EVENT

Probability begins with some activity, process, or experiment whose outcome is uncertain. This can be as simple as throwing dice or as complicated as tomorrow’s weather.

Given such a “random experiment,” the set of all possible outcomes is called the sample space. We will use the Greek capital letter Ω (omega) to represent the sample space.

Perhaps the quintessential random experiment is flipping a coin. Suppose a coin is tossed three times. Let H represent heads and T represent tails. The sample space is

consisting of eight outcomes. The Greek lowercase omega ω will be used to denote these outcomes, the elements of Ω.

An event is a set of outcomes. The event of getting all heads in three coin tosses can be written as

The event of getting at least two tails is

We take probabilities of events. But before learning how to find probabilities, first learn to identify the sample space and relevant event for a given problem.

Example 1.1 The weather forecast for tomorrow says rain. The amount of rainfall can be considered a random experiment. If at most 24 inches of rain will fall, then the sample space is the interval Ω The event that we get between 2 and 4 inches of rain is A = [2.4].

Example 1.2 Roll a pair of dice. Find the sample space and identify the event that the sum of the two dice is equal to 7.

The random experiment is rolling two dice. Keeping track of the roll of each die gives the sample space

The event is A = {Sum is 7} = {(1.6). (2.5). (3.4). (4.3). (5. 2). (6.1)}.

Example 1.3 Yolanda and Zach are running for president of the student association. One thousand students will be voting. We will eventually ask questions like, What is the probability that Yolanda beats Zach by at least 100 votes? But before actually finding this probability, first identify (i) the sample space and (ii) the event that Yolanda beats Zach by at least 100 votes.

(i) The outcome of the vote can be denoted as (x. 1000 − x), where x is the number of votes for Yolanda, and 1000 − x is the number of votes for Zach. Then the sample space of all voting outcomes is

(ii) Let A be the event that Yolanda beats Zach by at least 100 votes. The event A consists of all outcomes in which x − (1000 − x) ≥ 100, or 550 ≤ x ≤ 1000. That is, A = {(550. 450). (551.449),…, (999.1). (1000. 0)}.

Example 1.4 Joe will continue to flip a coin until heads appears. Identify the sample space and the event that it will take Joe at least three coin flips to get a head.

The sample space is the set of all sequences of coin flips with one head preceded by some number of tails. That is,

The desired event is A = {TTH, TTTH, TTTTH,…}. Note that in this case both the sample space and the event A are infinite.

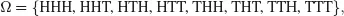
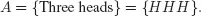
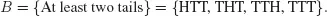
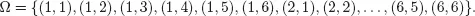
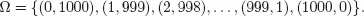
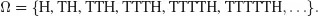
1.2 WHAT IS A PROBABILITY?

What does it mean to say that the probability that A occurs is equal to x?

From a formal, purely mathematical point of view, a probability is a number between 0 and 1 that satisfies certain properties, which we will describe later. From a practical, empirical point of view, a probability matches up with our intuition of the likelihood or “chance” that an event occurs. An event that has probability 0 “never” happens. An event that has probability 1 is “certain” to happen. In repeated coin flips, a coin comes up heads about half the time, and the probability of heads is equal to one-half.

Let A be an event associated with some random experiment. One way to understand the probability of A is to perform the following thought exercise: imagine conducting the experiment over and over, infinitely often, keeping track of how often A occurs. Each experiment is called a trial. If the event A occurs when the experiment is performed, that is a success. The proportion of successes is the probability of A, written P(A).

This is the relative frequency interpretation of probability, which says that the probability of an event is equal to its relative frequency in a large number of trials.

When the weather forecaster tells us that tomorrow there is a 20% chance of rain, we understand that to mean that if we could repeat today’s conditions—the air pressure, temperature, wind speed, etc.—over and over again, then 20% of the resulting “tomorrows” will result in rain. Closer to what weather forecasters actually do in coming up with that 20% number, together with using satellite and radar information along with sophisticated computational models, is to go back in the historical record and find other days that match up closely with ...

Table of contents

• COVER
• TITLE PAGE
• COPYRIGHT PAGE
• DEDICATION
• PREFACE
• ACKNOWLEDGEMENT
• INTRODUCTION
• 1 FIRST PRINCIPLES
• 2 CONDITIONAL PROBABILITY
• 3 INDEPENDENCE AND INDEPENDENT TRIALS
• 4 RANDOM VARIABLES
• 5 A BOUNTY OF DISCRETE DISTRIBUTIONS
• 6 CONTINUOUS PROBABILITY
• 7 CONTINUOUS DISTRIBUTIONS
• 8 CONDITIONAL DISTRIBUTION, EXPECTATION, AND VARIANCE
• 9 LIMITS
• 10 ADDITIONAL TOPICS
• APPENDIX A: GETTING STARTED WITH R
• APPENDIX B: PROBABILITY DISTRIBUTIONS IN R
• APPENDIX C: SUMMARY OF PROBABILITY DISTRIBUTIONS
• APPENDIX D: REMINDERS FROM ALGEBRA AND CALCULUS
• APPENDIX E: MORE PROBLEMS FOR PRACTICE
• SOLUTIONS TO EXERCISES
• REFERENCES
• INDEX