The Elements of Continuum Biomechanics

Marcelo Epstein

• Publisher: Wiley
• Year: 2012
• Print ISBN: 9781119999232
• eBook ISBN: 9781118361009
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Mechanics

An appealing and engaging introduction to Continuum Mechanics in Biosciences

This book presents the elements of Continuum Mechanics to people interested in applications to biological systems. It is divided into two parts, the first of which introduces the basic concepts within a strictly one-dimensional spatial context. This policy has been adopted so as to allow the newcomer to Continuum Mechanics to appreciate how the theory can be applied to important issues in Biomechanics from the very beginning. These include mechanical and thermodynamical balance, materials with fading memory and chemically reacting mixtures.

In the second part of the book, the fully fledged three-dimensional theory is presented and applied to hyperelasticity of soft tissue, and to theories of remodeling, aging and growth. The book closes with a chapter devoted to Finite Element analysis. These and other topics are illustrated with case studies motivated by biomedical applications, such as vibration of air in the air canal, hyperthermia treatment of tumours, striated muscle memory, biphasic model of cartilage and adaptive elasticity of bone.  The book offers a challenging and appealing introduction to Continuum Mechanics for students and researchers of biomechanics, and other engineering and scientific disciplines.

Key features:

• Explains continuum mechanics using examples from biomechanics for a uniquely accessible introduction to the topic
• Moves from foundation topics, such as kinematics and balance laws, to more advanced areas such as theories of growth and the finite element method..
• Transition from a one-dimensional approach to the general theory gives the book broad coverage, providing a clear introduction for beginners new to the topic, as well as an excellent foundation for those considering moving to more advanced application

Part I

A One-Dimensional Context

Chapter 1

Material Bodies and Kinematics

1.1 Introduction

Many important biological structures can be considered as continuous, and many of these can be regarded as one-dimensional and straight. Moreover, it is not uncommon to observe that, whenever these structures deform, grow, sustain heat and undergo chemical reactions, they remain straight. Let us look at some examples.

Tendons. One of the main functions of tendons is to provide a connection between muscles (made of relatively soft tissue) and bone (hard tissue). Moreover, the deformability of tendinous tissue and its ability to store and release elastic energy are important for the healthy performance of human and animal activities, such as walking, running, chewing and eye movement. Tendons are generally slender and straight. Figure 1.1 shows a human foot densely populated by a network of tendons and ligaments. The Achilles tendon connects the calcaneus bone with the gastrocnemius and soleus muscles located in the lower leg.

Figure 1.1 Tendons and ligaments in the human foot

Muscle components. Most muscles are structurally too complex to be considered as one-dimensional entities. On the other hand, at some level of analysis, muscle fibres and their components down to the myofibril and sarcomere level can be considered as straight one-dimensional structural elements, as illustrated schematically in Figure 1.2.

Figure 1.2 A skeletal muscle and its components

Hair. Figure 1.3 shows a skin block with follicles and hair. When subjected to tensile loads, hair can be analysed as a one-dimensional straight structure.

Figure 1.3 Skin cube with follicles and hair

One of the questions that continuum mechanics addresses for these and more complex structures is the following: what is the mechanism of transmission of load? The general answer to this question is: deformation. It took millennia of empirical familiarity with natural and human-made structures before this simple answer could be arrived at. Indeed, the majestic Egyptian pyramids, the beautiful Greek temples, the imposing Roman arches, the overwhelming Gothic cathedrals and many other such structures were conceived, built and utilized without any awareness of the fact that their deformation, small as it might be, plays a crucial role in the process of transmission of load from one part of the structure to another. In an intuitive picture, one may say that the deformation of a continuous structure is the reflection of the change in atomic distances at a deeper level, a change that results in the development of internal forces in response to the applied external loads. Although this naïve model should not be pushed too far, it certainly contains enough physical motivation to elicit the general picture and to be useful in many applications.

Once the role of the deformation has been recognized, continuum mechanics tends to organize itself in a tripartite fashion around the following questions:

1. How is the deformation of a continuous medium described mathematically?

2. What are the physical laws applicable to all continuous media?

3. How do different materials respond to various external agents?

This subdivision of the discipline is not only paedagogically useful, but also epistemologically meaningful. The answers to the three questions just formulated are encompassed, respectively, under the following three headings:

1. continuum kinematics;

2. physical balance laws;

3. constitutive theory.

From the mathematical standpoint, continuum kinematics is a direct application of the branch of mathematics known as differential geometry. In the one-dimensional context implied by our examples so far, all that needs to be said about differential geometry can be summarily absorbed within the realm of elementary calculus and algebra. For this to be the case, it is important to bear in mind not only that the structures considered are essentially one-dimensional, but also that they remain straight throughout the process of deformation.

The physical balance laws that apply to all continuous media, regardless of their material constitution, are mechan...

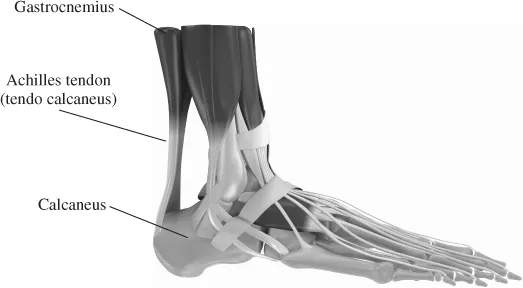
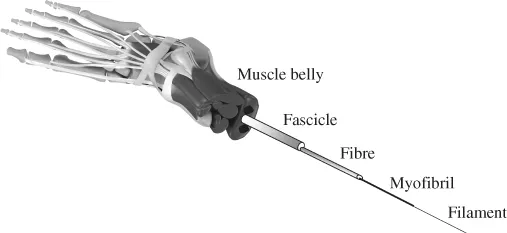
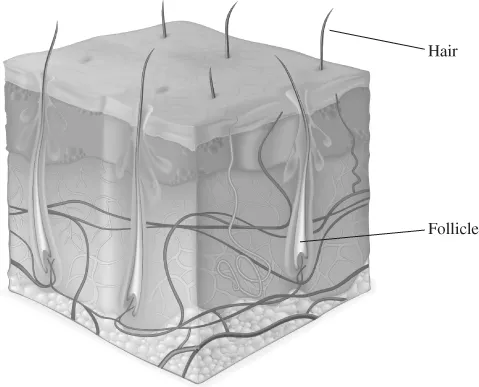
Table of contents

• Cover
• Title Page
• Copyright
• Dedication
• Preface
• Part I: A One-dimensional Context
• Part II: Towards Three Spatial Dimensions
• Index