Resource-Constrained Project Scheduling

Models, Algorithms, Extensions and Applications

Christian Artigues, Sophie Demassey, Emmanuel Néron, Christian Artigues, Sophie Demassey, Emmanuel Néron

• Publisher: Wiley-ISTE
• Year: 2013
• Print ISBN: 9781848210349
• eBook ISBN: 9781118623701
• Edition: 1
• Topic: Technology & Engineering
• Subtopic: Electrical Engineering & Telecommunications
• Index: Technology & Engineering

This title presents a large variety of models and algorithms dedicated to the resource-constrained project scheduling problem (RCPSP), which aims at scheduling at minimal duration a set of activities subject to precedence constraints and limited resource availabilities.
In the first part, the standard variant of RCPSP is presented and analyzed as a combinatorial optimization problem. Constraint programming and integer linear programming formulations are given. Relaxations based on these formulations and also on related scheduling problems are presented. Exact methods and heuristics are surveyed. Computational experiments, aiming at providing an empirical insight on the difficulty of the problem, are provided.
The second part of the book focuses on several other variants of the RCPSP and on their solution methods. Each variant takes account of real-life characteristics which are not considered in the standard version, such as possible interruptions of activities, production and consumption of resources, cost-based approaches and uncertainty considerations.
The last part presents industrial case studies where the RCPSP plays a central part. Applications are presented in various domains such as assembly shop and rolling ingots production scheduling, project management in information technology companies and instruction scheduling for VLIW processor architectures.

Part 1

Models and Algorithms for the Standard Resource-Constrained Project Scheduling Problem

Chapter 1

The Resource-Constrained Project Scheduling Problem ¹

1.1. A combinatorial optimization problem

Informally, a resource-constrained project scheduling problem (RCPSP) considers resources of limited availability and activities of known durations and resource requests, linked by precedence relations. The problem consists of finding a schedule of minimal duration by assigning a start time to each activity such that the precedence relations and the resource availabilities are respected.

More formally, the RCPSP can be defined as a combinatorial optimization problem. A combinatorial optimization problem is defined by a solution space χ, which is discrete or which can be reduced to a discrete set, and by a subset of feasible solutions

associated with an objective function

. A combinatorial optimization problem aims at finding a feasible solution

such that f(y) is minimized or maximized. A resource-constrained project scheduling problem is a combinatorial optimization problem defined by a tuple (V, p, E,

, B, b).

Activities constituting the project are identified by a set V = {A₀,…, A_n+1}. Activity A₀ represents by convention the start of the schedule and activity A_n+1 symmetrically represents the end of the schedule. The set of non-dummy activities is identified by

= {A₁,…, A_n}.

Durations are represented by a vector p in

ⁿ⁺² where p_i is the duration of activity A_i, with special values p₀ = p_n+1 = 0.

Precedence relations are given by E, a set of pairs such that (A_i, A_j) ∈ E means that activity A_i precedes activity A_j. A precedence activity-on-node graph G(V, E) is defined where nodes correspond to activities and arcs correspond to precedence relations¹. We assume that G contains no cycle, otherwise the precedence relations are obviously inconsistent. Since precedence is a transitive binary relation, the existence of a path in G from node A_i to node A_j also means that activity A_i precedes activity A_j. Thus, all precedence graphs having the same transitive closure define the same precedence constraints. We assume that, taking account of the preceding remark, E is such that A₀ is a predecessor of all other activities and A_n+1 is a successor of all other activities.

Renewable resources are formalized by set

= {R₁,…, R_q}.

Availabilities of resources are represented by a vector B in

^q such that B_k denotes the availability of R_k. In particular, a resource R_k such that R_k = 1 is called a unary or disjunctive resource. Otherwise, as a resource may process several activities at a time, it is called a cumulative resource.

Demands of activities for resources are abstracted by b, a (n+2)×q integer matrix, such that b_ik represents the amount of resource R_k used per time period during the execution of A_i.

A schedule is a point S in

ⁿ⁺² such that S_i represents the start time of activity A_i. C_i denotes the completion time of activity A_i, with C_i = S_i+p_i. S₀ is a reference point for the start of the project. Here we assume that S₀ = 0. A solution S is feasible if it is compatible with the precedence constraints (1.1) and the resource constraints (1.2) expressed below, where

represents the set of non-dummy activities in process at time t.

(1.1)

(1.2)

The makespan of a schedule S is equal to S_n+1, the start time of the end activity. The above-defined set

_t and constraints state that an activity cannot be interrupted once it is started. This is referred to as not allowing preemption². The RCPSP can then be stated as follows:

DEFINITION 1.1.- The RCPSP is the problem of finding a non-preemptive schedule S of minimal makespan S_n+1 subject to precedence constraints (1.1) and resource constraints (1.2).

An important preliminary remark is that, since durations are integers, we can restrict ourselves to integer schedules without missing the optimal solution. A non-integer feasible schedule can be transformed into an integer feasible schedule without increasing the makespan by recursively applying the following principle. Consider a non-integer schedule S and let A_i denote the first activity in the increasing start time order such that S_i ∉

. Then setting S_i to its nearest lower integer

does not violate any precedence constraints, since the completion time of the predecessors of A_i are integers strictly lower than S_i. Left shifting an activity can violate a resource constraint only if it enters new sets

for

. Since we have

for

, no resource-constraint violation can appear by setting S_i to

. The set of integer schedules, containing at least one optimal solution, is said to be dominant.

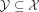
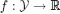
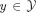
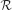
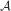
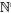
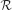
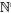
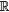
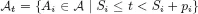
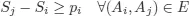
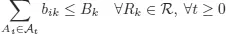
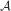
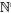
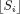
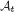
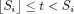
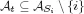
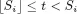
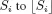
1.2. A simple resource-constrained project example

In Table 1.1, a RCPSP instance is given with n = 10 real activities and |

| = 2 resources with availabilities B₁ = 7 and B₂ = 4.

Table 1.1. A project with 10 real activities and 2 resources

The precedence constraints linking the activities A_i ∈ V are displayed in Figure 1.1 as an activity-on-node graph. A schedule of minimal makespan

is displayed in Figure 1.2 as a 2-dimensional Gantt chart where the x axis represents the time and the y axis represents the resource occupation.

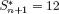
1.3. Computational complexity

According to the computational complexity theory [GAR 79], the RCPSP is one of the most intractable combinatorial optimization problems. Indeed, the RCPSP belongs to the class of problems t...

Table of contents

• Cover
• Title Page
• Copyright
• Preface
• Part 1: Models and Algorithms for the Standard Resource-Constrained Project Scheduling Problem
• Part 2: Variants and Extensions
• Part 3: Industrial Applications
• Bibliography
• List of Authors
• Index