Product Life-Cycle Management

Geometric Variations

Max Giordano, Luc Mathieu, François Villeneuve, Max Giordano, Luc Mathieu, François Villeneuve

• Publisher: Wiley-ISTE
• Year: 2012
• Print ISBN: 9781848212763
• eBook ISBN: 9781118587522
• Edition: 1
• Topic: Business
• Subtopic: Management
• Index: Business

This book gives a comprehensive view of the most recent major international research in the field of tolerancing, and is an excellent resource for anyone interested in Computer Aided Tolerating.

It is organized into 4 parts. Part 1 focuses on the more general problems of tolerance analysis and synthesis, for tolerancing in mechanical design and manufacturing processes. Part 2 specifically highlights the simulation of assembly with defects, and the influence of tolerances on the quality of the assembly. Part 3 deals with measurement aspects, and quality control throughout the life cycle. Different measurement technologies and methods for estimating uncertainty are considered. In Part 4, different aspects of tolerancing and their interactions are explored, from the definition of functional requirement to measurement processes in a PLM approach.

PART I

Tolerance Analysis and Synthesis

Chapter 1

A New Method of Expressing Functional Requirements and How to Allocate Tolerance to Parts ¹

This chapter proposes a new approach for expressing the functional requirement, based on the non-quality cost that can be non-symmetrical if necessary. This is very realistic from the point-of-view of functional requirements. Then a link between mean and variance of the functional dimension is identified for a chosen loss cost. Specifications on parts are expressed in a system of inequalities that link the means and variances of the functional dimensions. It is then possible to allocate the functional requirements on parts. To illustrate the concept, the case of application with unidirectional tolerancing is presented. The results are compared to the usual tolerancing approaches.

1.1. Introduction

When dealing with assembly tolerance synthesis, several key points can be identified such as the expression of the functional requirements, the identification of the dimension chains and then the allocation of the component tolerances. In this chapter, it is assumed that the dimension chains are identified, hence two key points are focused upon: the expression of the assembly functional requirements and the allocation of the tolerances for the assembly components.

The first part of this chapter is a short review of some existing statistical tolerancing methods. Two approaches are presented, traditional statistical tolerancing using tolerance interval, and inertial tolerancing. For each approach, their capability indices and several tolerancing methods are presented. In order to compare the different tolerancing methods, statistical tolerance zones and their composition are used. The case of application is also presented. It is based on a five component stack up, for which the functional requirement is a unidirectional combination of the component dimensions.

The second part of this chapter presents a new approach to the expression of the functional requirements and how to allocate component tolerances. The first key point concerning the functional requirement is presented. The functional requirements can either be symmetrical as usual or asymmetrical if necessary. Depending on the assumption of the assembly resultant distribution, the functional requirement can be transcribed into inequalities on the assembly resultant mean and variance. The second key point dealing with the allocation of the functional requirement on the assembly components is also presented in this first part. The only strategy presented here aims to maximize the variances of components.

The case of application illustrates all the presented tolerancing methods in the first and the second part, and performance indices are presented to compare the efficiency of the methods. The chapter then ends with a short discussion.

1.2. Brief review

This section presents the case of application and the statistical tolerance zone that are used to compare the different tolerancing approaches. The section then deals with some existing methods of statistical tolerancing with tolerance intervals.

1.2.1. How to compare

The following presents the application to which the tolerancing methods are applied, and a technique for tolerance analysis that enables us to qualify the efficiency of the tolerancing method.

1.2.1.1. The case of application

Figure 1.1. The case of application

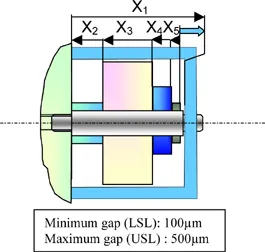
To illustrate the proposed method, a five component stack up is chosen as an application case. This mechanical example also enables us to apply and compare the existing tolerancing approaches briefly presented in this part. The functional requirement of the assembly mechanism is composed of two limits:

– a minimum gap of 100 µm, to allow the free rotation of the inner parts, then the good working condition of the mechanism;

– a maximum gap of 500 µm, to minimize the free translation of the inner parts, thus to minimize the noise while shaking the mechanism.

1.2.1.2. Statistical tolerance zones

In order to graphically compare the tolerance allocation results of the different tolerancing methods, the statistical tolerance zones (STZ) and their composition are used. This technique proposed by [SRI 97] allows us to describe each tolerance by a domain in the (μ, σ) plane. Within the (μ, σ²) plane, it is possible to convolute the domain of the possible deviation of the assembly resultant given the tolerance domain of the components. The assembly resultant domain can then be compared to its functional requirement domain. This method is used in this chapter to compute the assembly resultant domain for each tolerancing method.

This technique allows us to graphically compare each tolerancing method result to the functional requirement, and it is more interesting to compare one to the other. Two indices are introduced to qualify the efficiency of the tolerancing methods:

– R_NC, the ratio of the non-conforming area, that compares the area of the assembly resultant domain out of the functional requirement domain to the functional requirement domain area.

– R_exp, the exploitation ratio that compares the area of the assembly resultant domain inside the functional requirement domain to the functional requirement domain.

If the R_NC index equals 0, this means that the tolerancing approach offers no non-conforming configuration, thus it is a no-risk tolerancing method. If the R_exp index equals 1, this means that the entire assembly functional requirement domain is exploited by the tolerancing method. If the index R_NC equals 0 and R_exp equals 1, the result of the tolerancing approach perfectly fits the functional requirement domain.

1.2.2. Statistical tolerancing methods

The statistical tolerancing methods presented in this second section are applied to the...

Table of contents

• Cover
• Title Page
• Copyright
• Preface
• PART I: Tolerance Analysis and Synthesis
• PART II: Simulation of Assemblies
• PART III: Measurement
• PART IV: Tolerancing in the PLM
• List of Authors
• Index