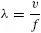Inductance

Loop and Partial

Clayton R. Paul

• Publisher: Wiley-IEEE Press
• Year: 2011
• ISBN:
  9781118211281
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Electromagnetism

The only resource devoted Solely to Inductance

Inductance is an unprecedented text, thoroughly discussing "loop" inductance as well as the increasingly important "partial" inductance. These concepts and their proper calculation are crucial in designing modern high-speed digital systems. World-renowned leader in electromagnetics Clayton Paul provides the knowledge and tools necessary to understand and calculate inductance.

Unlike other texts, Inductance provides all the details about the derivations of the inductances of various inductors, as well as:

• Fills the need for practical knowledge of partial inductance, which is essential to the prediction of power rail collapse and ground bounce problems in high-speed digital systems
  
  

• Provides a needed refresher on the topics of magnetic fields
  
  

• Addresses a missing link: the calculation of the values of the various physical constructions of inductors—both intentional inductors and unintentional inductors—from basic electromagnetic principles and laws
  
  

• Features the detailed derivation of the loop and partial inductances of numerous configurations of current-carrying conductors
  
  

With the present and increasing emphasis on high-speed digital systems and high-frequency analog systems, it is imperative that system designers develop an intimate understanding of the concepts and methods in this book. Inductance is a much-needed textbook designed for senior and graduate-level engineering students, as well as a hands-on guide for working engineers and professionals engaged in the design of high-speed digital and high-frequency analog systems.

1

INTRODUCTION

The concept of inductance is simple and straightforward. However, actual computation of the inductance of various physical structures and its implementation in an electric circuit model of that structure is often fraught with misconceptions and mistakes that prevent its correct calculation and use. This book is intended to ensure the correct understanding, calculation, and implementation of inductance.

1.1 HISTORICAL BACKGROUND

Knowledge of magnetism has a long history [3]. A type of iron ore called lodestone had been discovered in Magnesia in Asia. This material had some interesting properties of magnetic attraction at a distance of other ferromagnetic substances and was known to Plato and Socrates. In the sixteenth century, William Gilbert first postulated that Earth was a giant spherical magnet, and A. Kirchner, in the seventeenth century, demonstrated that the two poles of a magnet have equal strength. Pierre de Marricourt constructed a compass in 1629 that allowed the determination of the direction of the North Pole of the Earth. In 1750, John Mitchell determined the universal principle that force at a distance depends on the inverse square of the distance. At the beginning of the nineteenth century, Alessandro Volta developed a battery (called a pile). This allowed the production of a current in a conducting material such as a wire. In 1820, Hans Christian Oersted showed that a current in a wire caused the needle of a compass to deflect. Around the same time, Andre Ampere conducted a set of experiments, resulting in his famous law. At about the same time, Jean-Baptiste Biot and Felix Savart formulated their important law governing the magnetic fields produced by currents: the Biot-Savart law. So up to this time it was known that in addition to permanent magnets, a current would produce a magnetic field. In 1831, Michael Faraday discovered that a time-changing magnetic field would also produce a current in a closed loop of wire. This discovery formed the essential idea of the inductance of a current loop. James Clerk Maxwell unified all this knowledge of the magnetic field as well as the knowledge of the electric field in 1873 in his renowned set of equations.

Extensive work on the calculation of the magnetic field of various current distributions and the associated concept of inductance dates back to the late nineteenth and early twentieth centuries. In fact, Maxwell in his famous treatise discussed inductance in 1873 [23]. An enormous amount of work was published on the determination of inductance from 1900 to 1920. (See the extensive list of references on magnetic fields in the book by Weber [11] and on inductance in the book by Grover [14].) This early work on inductance at the turn of the century was spurred by the introduction of 60-Hz ac power and its generation, distribution, and use. Some books, particularly those of the early twentieth century, tended to give only formulas for the magnetic fields of various distributions of currents and their inductance with little or no detail about the derivation of formulas. In that era, computers did not exist, so that many of the books and papers simply gave tables of values for the magnetic field and inductance as a function of certain parameters. Another important purpose of this book is to show, in considerable detail, how the results for the magnetic fields and the inductance are derived. All details of each derivation are shown. At the end of the book is a list of significant references and further readings on the subject of the computation of magnetic fields and inductance of various current-carrying structures. References to these are denoted in brackets.

1.2 FUNDAMENTAL CONCEPTS OF LUMPED CIRCUITS

We construct lumped-circuit models of electrical structures using the concepts and models of resistance, capacitance, and inductance [1,2]. We then solve for the resulting voltages and currents of that particular interconnection of circuit elements using Kirchhoff’s voltage law (KVL) (which relates the various voltages of the particular interconnection of circuit elements), Kirchhoff’s current law (KCL) (which relates the various currents of the particular interconnection of circuit elements), and the laws of the circuit elements (which relate the voltages of each circuit element to its currents) [1,2]. It is important to keep in mind that these lumped-circuit models are valid only if the largest physical dimension of the circuit is “electrically short” (e.g., < ^λ/10), where a wavelength λ is defined as the ratio of the velocity of wave propagation (along the component attachment leads), v, and the frequency of the wave, f [3–6]:

(1.1)

If the medium in which the circuit is immersed and through which the waves propagate along the connection leads is free space (essentially, air), the velocity of propagation of those waves is the speed of light, which is approximately v₀ ≅ 3 × 10⁸ m/s. For a printed circuit board (PCB), the velocity of propagation of the waves traveling along the lands on that board is about 60% of that of free space, due to the interaction of the fields with the board substrate, and the wavelengths are consequently shorter than in free space. Hence, circuit dimensions on a PCB are electrically longer than in free space. For a sinusoidal wave in free space at a frequency of 300 MHz, a wavelength is 1 m. At frequencies below this, the wavelength is proportionately larger than 1 m, and for frequencies above this, the wavelength is proportionately smaller. For example, at a frequency of 3 MHz a wavelength in free space is 100 m, and at a frequency of 3 GHz a wavelength in free space is 10 cm. Hence, for lumped-circuit concepts to be valid for a circuit having a sinusoidal source of frequency 3 MHz, the maximum physical dimension of the circuit must be less than about 10 m or about 30 ft. Similarly, for a circuit having a sinusoidal source of frequency 3 GHz, the maximum physical dimension must be less than about 1 cm or about 0.4 inch for it to be modeled as a lumped circuit. Today’s digital electronics have clock and data rates on the order of 300 MHz to 3 GHz. But these digital waveforms have a spectral content consisting of harmonics (integer multiples) of the basic repetition rate, which are generally significant up to at least the fifth harmonic. Hence, a 300-MHz clock rate has spectral content up to at least 1.5 GHz, and a 3-GHz clock rate has spectral content up to at least 15 GHz! So the lumped-circuit models (and their constituent components of capacitance and inductance) that were so reliable some 10 years ago are becoming less valid today. This trend will no doubt continue in the future as the requirement for higher clock and data speeds continues to increase, and the reader should keep in mind this fundamental limitation of inductance, capacitance, and the lumped-circuit models that use these elements.

The laws governing the calculation of resistance, capacitance, and inductance are written in terms of the vectors of the five basic electromagnetic field vectors, which are summarized in Table 1.1. Therefore, if we are to correctly calculate and understand the ideas of capacitance and inductance of a physical structure as well as use them correctly to construct a lumped-circuit model of that structure, we must understand some elementary properties of vectors and some basic vector calculus concepts. Trying to circumvent the use of vector calculus ideas by relying on one’s life experiences to compute and interpret the meaning of the capacitance and inductance of a structure properly has caused many of the incorrect results and misunderstanding, as well as the numerous erroneous applications that are seen throughout the literature and in conversations with engineering professionals. References [3–6] give extensive details on vector algebra and vector calculus. The Appendix of this book contains a review of the vector algebra and vector calculus concepts that are required to understand and compute the inductance of all physical structures.

TABLE 1.1. Electromagnetic Field Vectors

Symbol	Vector	Units
J	Current density	A/m^2
	Electric field vectors
E	Electric field intensity	V/meter
D	Electric flux density	C/m^2
	Magnetic field vectors
H	Magnetic field intensity	A/meter
B	Magnetic flux density	Wb/m^2 = T

The lumped-circuit elements of resistance, capacitance, and inductance are derived fundamentally for static conditions. Capacitance is derived for conductors that are supporting charges whose positions on those conductors are fixed. Resistance as well as inductance are derived for currents that are not varying with time: that is, direct (dc) currents. For charge distributions and currents that do not vary with time, the electromagnetic field equations (Maxwell’s equations) that govern the field vectors simplify considerably. However, the resulting electrical elements of resistance, capacitance, and inductance can be used to construct lumped-circuit models of a structure whose currents and charge distributions vary with time. This is valid as long as the sources driving the circuit have frequency content such that the largest physical dimension of the circuit is electrically small (see Section 3.4).

To understand the computation of inductance (the main subject of this book), it is useful to understand the dual concept of capacitance and its calculation. The basic idea of ...

Table of contents

• Cover
• Title
• Copyright
• PREFACE
• 1: INTRODUCTION
• 2: MAGNETIC FIELDS OF DC CURRENTS (STEADY FLOW OF CHARGE)
• 3: FIELDS OF TIME-VARYING CURRENTS (ACCELERATED CHARGE)
• 4: THE CONCEPT OF “LOOP” INDUCTANCE
• 5: THE CONCEPT OF “PARTIAL” INDUCTANCE
• 6: PARTIAL INDUCTANCES OF CONDUCTORS OF RECTANGULAR CROSS SECTION
• 7: "LOOP" INDUCTANCE VS. "PARTIAL" INDUCTANCE
• APPENDIX: FUNDAMENTAL CONCEPTS OF VECTORS
• TABLE OF IDENTITIES, DERIVATIVES, AND INTEGRALS USED IN THIS BOOK
• REFERENCES AND FURTHER READINGS
• INDEX