Misconceptions of Risk

Terje Aven

• Publisher: Wiley
• Year: 2011
• Print ISBN: 9780470683880
• eBook ISBN: 9781119964285
• Edition: 1
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

We all face risks in a variety of ways, as individuals, businesses and societies. The discipline of risk assessment and risk management is growing rapidly and there is an enormous drive for the implementation of risk assessment methods and risk management in organizations. There are great expectations that these tools provide suitable frameworks for obtaining high levels of performance and balance different concerns such as safety and costs.

The analysis and management of risk are not straightforward. There are many challenges. The risk discipline is young and there area a number of ideas, perspectives and conceptions of risk out there. For example many analysts and researchers consider it appropriate to base their risk management policies on the use of expected values, which basically means that potential losses are multiplied with their associated consequences. However, the rationale for such a policy is questionable.

A number of such common conceptions of risk are examined in the book, related to the risk concept, risk assessments, uncertainty analyses, risk perception, the precautionary principle, risk management and decision making under uncertainty. The Author discusses these concepts, their strenghts and weaknesses, and concludes that they are often better judged as misconceptions of risk than conceptions of risk.

Key Features:

• Discusses common conceptions of risk with supporting examples.
• Provides recommendations and guidance to risk analysis and risk management.
• Relevant for all types of applications, including engineering and business.
• Presents the Author's overall conclusions on the issues addressed throughout the book.

All those working with risk-related problems need to understand the fundamental ideas and concepts of risk. Professionals in the field of risk, as well as researchers and graduate sutdents will benefit from this book. Policy makers and business people will also find this book of interest.

1

Risk is equal to the expected value

If you throw a die, the outcome will be either 1, 2, 3, 4, 5 or 6. Before you throw the die, the outcome is unknown – to use the terminology of statisticians, it is random. You are not able to specify the outcome, but you are able to express how likely it is that the outcome is 1, 2, 3, 4, 5 or 6. Since the number of possible outcomes is 6 and they are equally probable – the die is fair – the probability that the outcome turns out to be 3 (say), is 1/6. This is simple probability theory, which I hope you are familiar with.

Now suppose that you throw this die 600 times. What would then be the average outcome? If you do this experiment, you will obtain an average about 3.5. We can also deduce this number by some simple arguments: about 100 throws would give an outcome equal to 1, and this gives a total sum of outcomes equal to 100. Also about 100 throws would give an outcome equal to 2, and this would give a sum equal to 2 times 100, and so on. The average outcome would thus be

(1.1)

In probability theory this number is referred to as the expected value. It is obtained by multiplying each possible outcome with the associated probability, and summing over all possible outcomes. In our example this gives

(1.2)

We see that formula (1.2) is just a reformulation of (1.1) obtained by dividing 100 by 600 in each sum term of (1.1). Thus the expected value can be interpreted as the average value of the outcome of the experiment if the experiment is repeated over and over again. Statisticians would refer to the law of large numbers, which says that the average value converges to the expected value when the number of experiments goes to infinity.

Reflection

For the die example, show that the expected number of throws showing an outcome equal to 2 is 100 when throwing the die 600 times.

In each throw, there are two outcomes: one if the outcome is a ‘success’ (that is, shows 2), and zero if the outcome is a ‘failure’ (that is, does not show 2). The corresponding probabilities are 1/6 and 5/6. Hence the expected value for a throw equals 1 × 1/6 + 0 × 5/6 = 1/6, in other words the expected value equals the probability of a success. If you perform 2 throws the expected number of successes equals 2 × 1/6, and if you perform 600 throws the expected number of successes equals 600 × 1/6 = 100. These conclusions are intuitively correct and are based on a result from probability calculus saying that the expected value of a sum equals the sum of the expected values. Thus the desired result is shown.

The expected value is a key concept in risk analysis and risk management. It is common to express risk by expected values. Here are some examples:

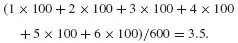
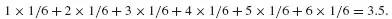
• For some experts ‘risk’ equals expected loss of life expectancy (HM Treasury, 2005, p. 33).
• Traditionally, hazmat transport risk is defined as the expected undesirable consequence of the shipment, that is, the probability of a release incident multiplied by its consequence (Verma and Verter, 2007).
• Risk is defined as the expected loss to a given element or a set of elements resulting from the occurrence of a natural phenomenon of a given magnitude (Lirer et al., 2001).
• Risk refers to the expected loss associated with an event. It is measured by combining the magnitudes and probabilities of all of the possible negative consequences of the event (Mandel, 2007).
• Terrorism risk refers to the expected consequences of an existent threat, which, for a given target, attack mode, target vulnerability and damage type, can be expressed as the probability that an attack occurs multiplied by the expected damage, given that an attack occurs (Willis, 2007).
• Flood risk is defined as expected flood damage for a given time period (Floodcite, 2006).

But is an expected value an adequate expression of risk? And should decisions involving risk be based on expected values?

Example. A Russian roulette type of game

Let us look at an example: a Russian roulette type of game where you are offered a play using a six-chambered revolver. A single round is placed in the revolver such that the location of the round is unknown. You take the weapon and shoot, and if it discharges, you lose $24 million. If it does not discharge, you win $6 million.

As the probability of losing $24 million is 1/6, and of winning $6 million is 5/6, the expected gain is given by

Thus the expected gain is $1 million. Say that you are not informed about the details of the game, just that the expected value equals $1 million. Would that be sufficient for you to make a decision whether to play or not play? Certainly not - you need to look beyond the expected value. The possible outcomes of the game and the associated probabilities are required to provide the basis for an informed decision. Would it not be more natural to refer to this information as risk, and in particular the probability that you lose $24 million? As we will see in coming chapters, such conceptions of risk are common.

The game has an expected value of $1 million, but that does not mean that you would accept the game as you may lose $24 million. The probability 1/6 of losing may be considered very high as such a loss could have dramatic consequences for you. And how important is it for you to win the $6 million? Perhaps your financial situation is good and an additional $6 million would not change your life very much for the better. The decision to accept the play needs to take into account aspects such as usefulness, desirability and satisfaction. Decision analysts and economists use the term utility to convey these aspects.

Daniel Bernoulli: The need to look beyond expected values

The observation that there is a need for seeing beyond the expected values in such decision-making situations goes back to Daniel Bernoulli (1700–1782) more than 250 years ago. In 1738, the Papers of the Imperial Academy of Sciences in St Petersburg carried an essay with this central theme: ‘the value of an item must not be based on its price, but rather on the utility that it yields’ (Bernstein, 1996). The author was Daniel Bernoulli, a Swiss mathematician who was then 38 years old. Bernoulli’s St Petersburg paper begins with a paragraph that sets forth the thesis that he aims to attack (Bernstein, 1996):

Ever since mathematicians first began to study the measurement of risk, there has been general agreement on the following proposition: Expected values are computed by multiplying each possible gain by the number of ways it can occur, and dividing the sum of these products by the total number of cases.

Bernoulli finds this thesis flawed as a description of how people in real life go about making decisions, because it focuses only on gains (prices) and probabilities, and not the utility o...

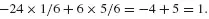
Table of contents

• Cover
• Title Page
• Copyright
• Preface
• Acknowledgements
• 1: Risk is equal to the expected value
• 2: Risk is a probability or probability distribution
• 3: Risk equals a probability distribution quantile (value-at-risk)
• 4: Risk equals uncertainty
• 5: Risk is equal to an event
• 6: Risk equals expected disutility
• 7: Risk is restricted to the case of objective probabilities
• 8: Risk is the same as risk perception
• 9: Risk relates to negative consequences only
• 10: Risk is determined by the historical data
• 11: Risk assessments produce an objective risk picture
• 12: There are large inherent uncertainties in risk analyses
• 13: Model uncertainty should be quantified
• 14: It is meaningful and useful to distinguish between stochastic and epistemic uncertainties
• 15: Bayesian analysis is based on the use of probability models and Bayesian updating
• 16: Sensitivity analysis is a type of uncertainty analysis
• 17: The main objective of risk management is risk reduction
• 18: Decision-making under uncertainty should be based on science (analysis)
• 19: The precautionary principle and risk management cannot be meaningfully integrated
• 20: Conclusions
• Index