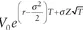Retirement Portfolios Workbook

Theory, Construction, and Management

Michael J. Zwecher

• Publisher: Wiley
• Year: 2009
• Print ISBN: 9780470559871
• eBook ISBN: 9780470586228
• Edition: 1
• Topic: Business
• Subtopic: Investments & Securities
• Index: Business

A companion Workbook to the text Retirement Portfolios

Retirement is one of the most important parts of the financial planning process. Yet only two percent of financial advisors describe themselves as competent in retirement planning.

Constructing a retirement portfolio is viewed as a difficult endeavor, and the demands facing financial advisors responsible for this task continue to grow. The pressures are particularly intense due to events such as the financial crisis and oncoming rush of retiring baby boomers. It is imperative that financial advisors be equipped and ready to create appropriate retirement portfolios. That's why Michael Zwecher-a leading expert on retirement income-has created Retirement Portfolios and the Retirement Portfolios Workbook. In the text Retirement Portfolios, leading retirement income expert Michael Zwecher provides financial professionals with complete coverage of the most important issues in this field. The Retirement Portfolios Workbook offers you a wealth of practical information and exercises that will solidify your understanding of the tools and techniques associated with this discipline. This comprehensive study guide

• Provides chapter summaries and end of chapter questions to the main book
• Test your knowledge of the information addressed in Retirement Portfolios, before you put it to work in real world situations
• Helps you learn to solve problems while setting up tools you can use in practice
• Puts the management of risks related to retirement portfolios in perspective

If you want to gain a firm understanding of the information outlined in Retirement Portfolios, the lessons within this workbook can show you how.

PART One

Questions

CHAPTER 1

Portfolio Focus and Stage of Life

Contents

A “Balanced” Portfolio Approach May Not Last Through Retirement

Fixing Spending Levels (Variable Weights) and Shortfall Risk

Fixing Depletion Weights (Variable Spending) and Lifestyle Risk

Falling for Murphy’s Law of Timing Retirement

Drawdown Plans Are Sensitive to Longevity

Retirement Saving versus Retirement Income: An Illustration
Products versus Solutions

Objectives

Why retirement income planning differs from accumulation
The danger of drawdown plans

CHAPTER RECAP

This chapter showed that traditional portfolios, built for accumulation of wealth, frequently fail during withdrawal in retirement. In a nutshell, the problem is that traditional portfolios are designed around the principle of finding what is, on average, the best alternative—and finding the best portfolio for an individual client out of those that will not fail. These first few examples are designed to reinforce the notions that drawdown plans suffer from major weaknesses.

• When making withdrawals the order of returns matters

• The timing of retirement can have a significant impact on the likelihood of success or failure

• Unexpected shocks, even one-time shocks, can destroy a plan

• Outliving one’s assets becomes a more acute risk for an “optimized” withdrawal strategy

PROBLEMS

Our purpose here is to examine what does and does not work. For simplicity, we assume throughout this chapter that each client is at the point of retirement. A secondary purpose of these problems is to gently brush away cobwebs that you may have acquired with some refresher exercises geared to the material at hand.

Problems 1-10 refer to the following set of returns data and assume that the starting portfolio value is $1,000,000:

Period	Return
1	10%
2	-10%
3	-10 %
4	10%
5	-10%
6	-10%
7	-10%
8	-10 %
9	-10 %
10	-10%
11	-10%
12	-10%
13	10%
14	30%
15	30%
16	30%
17	30%
18	30%
19	30%
20	30%

1. Find the arithmetic average return over the 20-year sample period.

2. Find the geometric average return over the 20-year sample period.

3. For an accumulation portfolio, assume that the client, the Scott family, starts with $1 million and saves an additional $50,000 per year at the beginning of each year for each of the next 20 years. Find the value of the Scott’s portfolio, assuming the return stream above, at the end of 20 years.

4. Assuming the data from Problem 3, find the geometric average of growth rate for the net increase in the Scott’s portfolio value.

5. Suppose that a client, the Andrews family, wants to draw down the $1,000,000 family portfolio by $50,000 per year. Withdrawals will be made at the beginning of the year. If the Andrews put the remaining money in a checking account earning 2 percent, find whether the funds will last for 20 years.

6. Suppose that the breadwinner in the Petrocelli family is retiring and the family wants to draw down the $1,000,000 portfolio by $50,000 per year. Withdrawals will be made at the end of the period. If the Petrocellis put the money in an account comprised of the risky assets with the return stream provided in Problem 1, find whether the funds will last for 20 years or whether they come up short.

7. Another client, the Foys, have perfect foresight and know the return stream given at the start of this section will occur. To the nearest $250, find the maximum annual withdrawal that the Foys can take from the account that will be guaranteed to last for 20 years.

8. The Howard family has $1,000,000 and will invest in the risky portfolio given at the start of this section. They are willing to adjust their retirement lifestyle each year to make sure that the money lasts for 20 years. To achieve their goal, they will draw down the portfolio at the beginning of each year by 1/the remaining number of years, that is, 1/20, 1/19, 1/18, ..., 1/2, 1. Show how much the Howard family receives in income in each year.

9. Using a flat 3 percent yield curve for Treasury securities, find the present value of a 20-year annuity that pays $50,000 at the beginning of each period.

10. The Smiths want to make sure that they are covered. They purchase Treasury securities that will pay them $50,000 per year and put the rest in a portfolio that has the return stream given previously. The Treasury yield curve is flat at 3 percent. They will draw down their risky account at the beginning of each period as the Howards have done in Problem 8. Find their annual income.

Research analysts have a feeling that the next period will bring returns of 40 percent. Suppose that they are correct, but that the remaining returns for periods 2-20 are as given in the table at the start of this section.

11. Find the simple sample average return for the 20-year period assuming a 40 percent return in period 1.

12. Find the geometric average return for the 20-year period assuming a 40 percent return in period 1.

13. The Tartabull family will be drawing down $1,000,000 at $50,000 per year at the beginning of the year. Determine whether the inclusion of a 40 percent return in period 1 is sufficient to enable a successful drawdown scheme.

14. Suppose that the information is as in Problem 13, but the withdrawals are made at the end of the year. Determine whether the inclusion of a 40 percent return in period 1 is sufficient to enable a successful drawdown scheme.

15. The Tiants are not sure how long they will live. After seeing what the Smiths had planned (Problem 10) they have decided with their adviser that they will live on $50,000 per year, received at the beginning of the year. Their adviser will create $50,000 in income for them using Treasury securities and will place the unallocated funds in a risky account with the returns stream as in Problems 1-9. At the end of the 20-year period, find how much they will have left over to fund potential longevity.

Use the following information for Problems 16 and 17:

Many portfolio books concentrate on the distribution of returns, which they assume to be normal. The following will help show how prices and portfolio values evolve if returns are normally distributed, how risky returns impact portfolio values, and briefly discuss the asymmetry of the distribution of portfolio values.

16. Your client, the Lonborgs have a $1,000,000 portfolio that follows the process V_T =

. They are considering whether to place their funds in a riskless asset yielding an APR of 3 percent. Find the portfolio value that would result after 20 years if they place the funds in a risk-free account. Also, find the values if they place their funds in a risky portfolio with r = 7 percent, σ = 12 percent, resulting in the following outcomes: Z values Z = -1.645, Z = 1.645 (corresponding to the points where 5 percent of portfolios would fall below and 5 percent would lie above if the assumed distribution is correct).

17. Suppose that you manage a $1,000,000 for your client, the Yastrzemskis. The portfolio is designed to provide an expected return of 8 percent (continuously compounded—this works out to an APR of e^0.08 - 1 = 8.329 percent) with a standard deviation of 15 percent per year. Provide the expected value of the portfolio and the dollar standard deviation sixteen years fro...

Table of contents

• Title Page
• Copyright Page
• Preface
• PART One - Questions
• PART Two - Solutions