A First Course in Wavelets with Fourier Analysis

Albert Boggess, Francis J. Narcowich

• Publisher: Wiley
• Year: 2011
• Print ISBN: 9780470431177
• eBook ISBN: 9781118211151
• Edition: 2
• Topic: Matematica
• Subtopic: Analisi matematica

A comprehensive, self-contained treatment of Fourier analysis and wavelets—now in a new edition

Through expansive coverage and easy-to-follow explanations, A First Course in Wavelets with Fourier Analysis, Second Edition provides a self-contained mathematical treatment of Fourier analysis and wavelets, while uniquely presenting signal analysis applications and problems. Essential and fundamental ideas are presented in an effort to make the book accessible to a broad audience, and, in addition, their applications to signal processing are kept at an elementary level.

The book begins with an introduction to vector spaces, inner product spaces, and other preliminary topics in analysis. Subsequent chapters feature:

• The development of a Fourier series, Fourier transform, and discrete Fourier analysis

• Improved sections devoted to continuous wavelets and two-dimensional wavelets

• The analysis of Haar, Shannon, and linear spline wavelets

• The general theory of multi-resolution analysis

• Updated MATLAB code and expanded applications to signal processing

• The construction, smoothness, and computation of Daubechies' wavelets

• Advanced topics such as wavelets in higher dimensions, decomposition and reconstruction, and wavelet transform

Applications to signal processing are provided throughout the book, most involving the filtering and compression of signals from audio or video. Some of these applications are presented first in the context of Fourier analysis and are later explored in the chapters on wavelets. New exercises introduce additional applications, and complete proofs accompany the discussion of each presented theory. Extensive appendices outline more advanced proofs and partial solutions to exercises as well as updated MATLAB routines that supplement the presented examples.

A First Course in Wavelets with Fourier Analysis, Second Edition is an excellent book for courses in mathematics and engineering at the upper-undergraduate and graduate levels. It is also a valuable resource for mathematicians, signal processing engineers, and scientists who wish to learn about wavelet theory and Fourier analysis on an elementary level.

1

FOURIER SERIES

1.1 INTRODUCTION

In this chapter, we examine the trigonometric expansion of a function f(x) defined on an interval such as –π ≤ x ≤ π. A trigonometric expansion is a sum of the form

(1.1)

where the sum could be finite or infinite. Why should we care about expressing a function in such a way? As the following sections show, the answer varies depending on the application we have in mind.

1.1.1 Historical Perspective

Trigonometric expansions arose in the 1700s, in connection with the study of vibrating strings and other, similar physical phenomena; they became part of a controversy over what constituted a general solution to such problems, but they were not investigated in any systematic way. In 1808, Fourier wrote the first version of his celebrated memoir on the theory of heat, Théorie Analytique de la Chaleur, which was not published until 1822. In it, he made a detailed study of trigonometric series, which he used to solve a variety of heat conduction problems.

Fourier’s work was controversial at the time, partly because he did make unsubstantiated claims and overstated the scope of his results. In addition, his point of view was new and strange to mathematicians of the day. For instance, in the early 1800s a function was considered to be any expression involving known terms, such as powers of x, exponential functions, and trigonometric functions. The more abstract definition of a function (i.e., as a rule that assigns numbers from one set, called the domain, to another set, called the range) did not come until later. Nineteenth-century mathematicians tried to answer the following question: Can a curve in the plane, which has the property that each vertical line intersects the curve at most once, be described as the graph of a function that can be expressed using powers of x, exponentials, and trigonometric functions. In fact, they showed that for “most curves,” only trigonometric sums of the type given in (1.1) are needed (powers of x, exponentials, and other types of mathematical expressions are unnecessary). We shall prove this result in Theorem 1.22.

The Riemann integral and the Lebesgue integral arose in the study of Fourier series. Applications of Fourier series (and the related Fourier transform) include probability and statistics, signal processing, and quantum mechanics. Nearly two centuries after Fourier’s work, the series that bears his name is still important, practically and theoretically, and still a topic of current research. For a fine historical summary and further references, see John J. Benedetto’s book (Benedetto, 1997).

1.1.2 Signal Analysis

There are many practical reasons for expanding a function as a trigonometric sum. If f(t) is a signal, (for example, a time-dependent electrical voltage or the sound coming from a musical instrument), then a decomposition of f into a trigonometric sum gives a description of its component frequencies. Here, we let t be the independent variable (representing t...

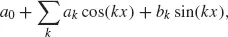
Table of contents

• Cover
• Title Page
• Copyright
• PREFACE AND OVERVIEW
• 0: INNER PRODUCT SPACES
• 1: FOURIER SERIES
• 2: THE FOURIER TRANSFORM
• 3: DISCRETE FOURIER ANALYSIS
• 4: HAAR WAVELET ANALYSIS
• 5: MULTIRESOLUTION ANALYSIS
• 6: THE DAUBECHIES WAVELETS
• 7: OTHER WAVELET TOPICS
• APPENDIX A: TECHNICAL MATTERS
• APPENDIX B: SOLUTIONSTOSELECTED EXERCISES
• APPENDIX C: MATLAB® ROUTINES
• BIBLIOGRAPHY
• INDEX