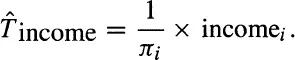Complex Surveys

A Guide to Analysis Using R

Thomas Lumley

• Publisher: Wiley
• Year: 2011
• ISBN:
  9781118210932
• Edition: 1
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

A complete guide to carrying out complex survey analysis using R

As survey analysis continues to serve as a core component of sociological research, researchers are increasingly relying upon data gathered from complex surveys to carry out traditional analyses. Complex Surveys is a practical guide to the analysis of this kind of data using R, the freely available and downloadable statistical programming language. As creator of the specific survey package for R, the author provides the ultimate presentation of how to successfully use the software for analyzing data from complex surveys while also utilizing the most current data from health and social sciences studies to demonstrate the application of survey research methods in these fields.

The book begins with coverage of basic tools and topics within survey analysis such as simple and stratified sampling, cluster sampling, linear regression, and categorical data regression. Subsequent chapters delve into more technical aspects of complex survey analysis, including post-stratification, two-phase sampling, missing data, and causal inference. Throughout the book, an emphasis is placed on graphics, regression modeling, and two-phase designs. In addition, the author supplies a unique discussion of epidemiological two-phase designs as well as probability-weighting for causal inference. All of the book's examples and figures are generated using R, and a related Web site provides the R code that allows readers to reproduce the presented content. Each chapter concludes with exercises that vary in level of complexity, and detailed appendices outline additional mathematical and computational descriptions to assist readers with comparing results from various software systems.

Complex Surveys is an excellent book for courses on sampling and complex surveys at the upper-undergraduate and graduate levels. It is also a practical reference guide for applied statisticians and practitioners in the social and health sciences who use statistics in their everyday work.

CHAPTER 1

BASIC TOOLS

In which we meet the probability sample and the R language.

1.1 GOALS OF INFERENCE

1.1.1 Population or process?

The mathematical development for most of statistics is model-based, and relies on specifying a probability model for the random process that generates the data. This can be a simple parametric model, such as a Normal distribution, or a complicated model incorporating many variables and allowing for dependence between observations. To the extent that the model represents the process that generated the data, it is possible to draw conclusions that can be generalized to other situations where the same process operates. As the model can only ever be an approximation, it is important (but often difficult) to know what sort of departures from the model will invalidate the analysis.

The analysis of complex survey samples, in contrast, is usually design-based. The researcher specifies a population, whose data values are unknown but are regarded as fixed, not random. The observed sample is random because it depends on the random selection of individuals from this fixed population. The random selection procedure of individuals (the sample design) is under the control of the researcher, so all the probabilities involved can, in principle, be known precisely. The goal of the analysis is to estimate features of the fixed population, and design-based inference does not support generalizing the findings to other populations.

In some situations there is a clear distinction between population and process inference. The Bureau of Labor Statistics can analyze data from a sample of the US population to find out the distribution of income in men and women in the US. The use of statistical estimation here is precisely to generalize from a sample to the population from which it was taken.

The University of Washington can analyze data on its faculty salaries to provide evidence in a court case alleging gender discrimination. As the university’s data are complete there is no uncertainty about the distribution of salaries in men and women in this population. Statistical modelling is needed to decide whether the differences in salaries can be attributed to valid causes, in particular to differences in seniority, to changes over time in state funding, and to area of study. These are questions about the process that led to the salaries being the way they are.

In more complex analyses there can be something of a compromise between these goals of inference. A regression model fitted to blood pressure data measured on a sample from the US population will provide design-based conclusions about associations in the US population. Sometimes these design-based conclusions are exactly what is required, e.g., there is more hypertension in blacks than in whites. Often the goal is to find out why some people have high blood pressure: is the racial difference due to diet, or stress, or access to medical care, or might there be a genetic component?

1.1.2 Probability samples

The fundamental statistical concept in design-based inference is the probability sample or random sample. In everyday speech, “taking a random sample” of 1000 individuals means a sampling procedure when any subset of 1000 people from the population is equally likely to be selected. The technical term for this is a “simple random sample”. The Law of Large Numbers implies that the sample of 1000 people is likely to be representative of the population, according to essentially any criteria we are interested in. If we compute the mean age, or the median income, or the proportion of registered Republican voters in the sample, the answer is likely to be close to the value for the population.

We could also end up with a sample of 1000 individuals from the US population, for example, by taking a simple random sample of 20 people from each state. On many criteria this sample is unlikely to be representative, because people from states with low populations are more likely to be sampled. Residents of these states have a similar age distribution to the country as a whole but tend to have lower incomes and be more politically conservative. As a result the mean age of the sample will be close to the mean age for the US population, but the median income is likely to be lower, and the proportion of registered Republican voters higher than for the US population. As long as we know the population of each state, this stratified random sample is still a probability sample. Yet another approach would be to choose a simple random sample of 50 counties from the US and then sample 20 people from each county. This sample would over-represent counties with low populations, which tend to be in rural areas. Even so, if we know all the counties in the US, and if we can find the number of households in the counties we choose, this is also a probability sample.

It is important to remember that what makes a probability sample is the procedure for taking samples from a population, not just the data we happen to end up with.

The properties we need of a sampling method for design-based inference are as follows:

1. Every individual in the population must have a non-zero probability of ending up in the sample (written π_i for individual i)

2. The probability π_i must be known for every individual who does end up in the sample.

3. Every pair of individuals in the sample must have a non-zero probability of both ending up in the sample (written π_ij for the pair of individuals (i,j)).

4. The probability π_ij must be known for every pair that does end up in the sample.

The first two properties are necessary in order to get valid population estimates; the last two are necessary to work out the accuracy of the estimates. If individuals were sampled independently of each other the first two properties would guarantee the last two, since then π_ij = π_iπ_j, but a design that sampled one random person from each US county would have π_i > 0 for everyone in the US and π_ij = 0 for two people in the same county. In the survey package, as in most software for analysis of complex samples, the computer will work out π_ij from the design description, they do not need to be specified explicitly.

The world is imperfect in many ways, and the necessary properties are present only as approximations in real surveys. A list of residences for sampling will include some that are not inhabited and miss some that have been newly constructed. Some people (me, for example) do not have a landline telephone, others may not be at home or may refuse to answer some or all of the questions. We will initially ignore these problems, but aspects of them are addressed in Chapters 7 and 9.

1.1.3 Sampling weights

If we take a simple random sample of 3500 people from California (with total population 35 million) then any person in California has a 1/10000 chance of being sampled, so π_i = 3500/3500000 = 1/10000 for every i. Each of the people we sample represents 10000 Californians. If it turns out that 400 of our sample have high blood pressure and 100 are unemployed, we would expect 400 × 10000 = 4 million people with high blood pressure and 100 × 10000 = 1 million unemployed in the whole state. If we sample 3500 people from Connecticut (population 3,500,000), all the sampling probabilities are equal to 3500/3500000 = 1/1000, so each person in the sample represents 1000 people in the population. If 400 of the sample had high blood pressure we would expect 400 × 1000 = 400000 people with high blood pressure in the state population.

The fundamental statistical idea behind all of design-based inference is that an individual sampled with a sampling probability of π_i represents 1/π_i individuals in the population. The value 1/π_i is called the sampling weight.

This weighting or “grossing up” operation is easy to grasp for a simple random sample where the probabilities are the same for every one. It is less obvious that the same rule applies when the sampling probabilities can be different. In particular, it may not be intuitive that the sampling probabilities for individuals who were not sampled do not need to be known.

Consider measuring income on a sample of one individual from a population of N, where π_i might be different for each individual. The estimate (

income) of the total income of the population (T income) would be the income for that individual multiplied by the sampling weight:

This will not be a very good estimate, since it is based on only one person, but it will be unbiased: the expected value of the estimate will equal the true population ...