Music and Acoustics

From Instrument to Computer

Philippe Guillaume

• Publisher: Wiley-ISTE
• Year: 2013
• Print ISBN: 9781905209262
• eBook ISBN: 9781118613993
• Edition: 1
• Topic: Sciences physiques
• Subtopic: Physique

How can a piano tuner obtain such high precision with no other measuring device than their own ears? How can a sequence of notes seem to rise continuously despite coming back periodically to the same notes? What are the possibilities and the limits of digital sound? These are a few examples of questions that are discussed in this book, which presents an overview on the nature of musical sounds, from their production by acoustic music instruments to synthesized sounds obtained with computers.
The topics that are treated include sound propagation, Fourier and time-frequency analysis, psychoacoustics, analog and digital signal processing theory, computer science and MP3 sound compression, and of course... music!

Chapter 1

Sounds

Sound and air are closely related: it is common knowledge that the Moonians (the inhabitants of the Moon) have no ears! This means we will begin our study of sound with the physics of its traveling medium: air. Sounds that propagate through our atmosphere consist of a variation of the air’s pressure p(x, y, z, t) according to position in space x, y and z and to the time t. It is these variations in pressure that our ears can perceive. In this chapter, we will first study how these sounds propagate as waves. We will then describe a few different types of sounds and various ways of representing them. Finally, we will explain the concept of filtering, which allows certain frequencies to be singled-out.

1.1. Sound propagation

The propagation of a sound wave can occur in any direction, and depends on the obstacles in its path. We will essentially be focusing on plane waves, that is to say waves that only depend on one direction of space. We will assume that this direction is the x-axis, and therefore that the pressure p(x, y, z, t) is independent of y and z. Hence it can simply be denoted by p(x, t). This type of function represents a plane wave propagating through space, but also a sound wave inside a tube (see Figure 1.1), such as for example the one propagating through an organ pipe.

1.1.1. A look at the physical models

The propagation of sound through air is governed by the wave equation (see page 21), an equation we will come across several times since it also determines the movement of sound waves in the vibrating parts (strings, membranes, tubes...) of many instruments. In the following paragraphs, we will see that, in the case of air, this equation is inferred from three fundamental equations of continuum mechanics.

Figure 1.1. Pressure waves in a tube open at its right end, with pressure imposed at the other end

Along with the pressure p(x, t), we rely on two other variables to describe the state of air: its density ρ(x, t), and the average speed v(x, t) of the air molecules set in motion by the sound wave, which is not to be confused with the norm of the individual speed of each molecule due to thermal agitation, the magnitude of which is close to that of the speed of sound, denoted by c. In the case of the plane wave that we are studying, the air moves in a direction parallel to the Ox-axis, and both the speed υ, and the pressure are independent of y and z. In the absence of an atmospheric perturbation, υ varies around the average value 0, and p and ρ vary around their average values ρ₀ and ρ₀ (see section 1.1.2), that is to say, their values in the equilibrium state: silence.

1.1.1.1. Mass conservation

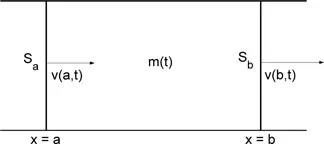
In a fixed section of space, bounded by a cylinder with its axis parallel to the Ox axis and the two surfaces S_a and S_b, with respective x-coordinates a and b and areas S (see Figure 1.2), the variation of the air mass m(t) is due to the amount of air going through the two surfaces. Nothing goes through the other interfaces, because the speed is parallel to the Ox axis. The air mass located inside the section is

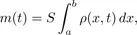
and the variation of the air mass per unit of time is the derivative of m(t), denoted by m′(t). The incoming flux through S_a, that is to say, the amount of air entering the section per unit of time, is equal to Sρ(a, t)v(a, t). As for the incoming flux through S_b, it is equal to –Sρ(b, t)v(b, t), the change of sign being due to the fact that we are calculating the balance of what is entering the section (and not of what is going from left to right). The total flux is therefore

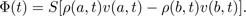
Figure 1.2. Mass balance in the air section: there is no disappearance or creation of air!

The fact that the total flux Φ(t) is the derivative of the mass m(t),

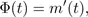
can be expressed, if ∂t denotes the partial derivative with respect to t, by

...

Table of contents

• Cover
• Title Page
• Copyright
• Dedication
• Foreword
• Chapter 1: Sounds
• Chapter 2: Music Instruments
• Chapter 3: Scales and Temperaments
• Chapter 4: Psychoacoustics
• Chapter 5: Digital Sound
• Chapter 6: Synthesis and Sound Effects
• Bibliography
• Index