Robust Statistics

Peter J. Huber, Elvezio M. Ronchetti

• Publisher: Wiley
• Year: 2011
• Print ISBN: 9780470129906
• eBook ISBN: 9781118210338
• Edition: 2
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

A new edition of the classic, groundbreaking book on robust statistics

Over twenty-five years after the publication of its predecessor, Robust Statistics, Second Edition continues to provide an authoritative and systematic treatment of the topic. This new edition has been thoroughly updated and expanded to reflect the latest advances in the field while also outlining the established theory and applications for building a solid foundation in robust statistics for both the theoretical and the applied statistician.

A comprehensive introduction and discussion on the formal mathematical background behind qualitative and quantitative robustness is provided, and subsequent chapters delve into basic types of scale estimates, asymptotic minimax theory, regression, robust covariance, and robust design. In addition to an extended treatment of robust regression, the Second Edition features four new chapters covering:

• Robust Tests
  
  

• Small Sample Asymptotics
  
  

• Breakdown Point
  
  

• Bayesian Robustness
  
  

An expanded treatment of robust regression and pseudo-values is also featured, and concepts, rather than mathematical completeness, are stressed in every discussion. Selected numerical algorithms for computing robust estimates and convergence proofs are provided throughout the book, along with quantitative robustness information for a variety of estimates. A General Remarks section appears at the beginning of each chapter and provides readers with ample motivation for working with the presented methods and techniques.

Robust Statistics, Second Edition is an ideal book for graduate-level courses on the topic. It also serves as a valuable reference for researchers and practitioners who wish to study the statistical research associated with robust statistics.

CHAPTER 1

GENERALITIES

1.1 WHY ROBUST PROCEDURES?

Statistical inferences are based only in part upon the observations. An equally important base is formed by prior assumptions about the underlying situation. Even in the simplest cases, there are explicit or implicit assumptions about randomness and independence, about distributional models, perhaps prior distributions for some unknown parameters, and so on.

These assumptions are not supposed to be exactly true—they are mathematically convenient rationalizations of an often fuzzy knowledge or belief. As in every other branch of applied mathematics, such rationalizations or simplifications are vital, and one justifies their use by appealing to a vague continuity or stability principle: a minor error in the mathematical model should cause only a small error in the final conclusions.

Unfortunately, this does not always hold. Since the middle of the 20th century, one has become increasingly aware that some of the most common statistical procedures (in particular, those optimized for an underlying normal distribution) are excessively sensitive to seemingly minor deviations from the assumptions, and a plethora of alternative “robust” procedures have been proposed.

The word “robust” is loaded with many—sometimes inconsistent—connotations. We use it in a relatively narrow sense: for our purposes, robustness signifies insensitivity to small deviations from the assumptions.

Primarily, we are concerned with distributional robustness : the shape of the true underlying distribution deviates slightly from the assumed model (usually the Gaussian law). This is both the most important case and the best understood one. Much less is known about what happens when the other standard assumptions of statistics are not quite satisfied and about the appropriate safeguards in these other cases.

The following example, due to Tukey (1960), shows the dramatic lack of distributional robustness of some of the classical procedures.

EXAMPLE 1.1

Assume that we have a large, randomly mixed batch of n “good” and “bad” observations x_i of the same quantity μ. Each single observation with probability 1 – ε is a “good” one, with probability ε a “bad” one, where ε is a small number. In the former case x_i is

(μ, σ²), in the latter

(μ, 9σ²). In other words all observations are normally distributed with the same mean, but the errors of some are increased by a factor of 3.

Equivalently, we could say that the x_i are independent, identically distributed with the common underlying distribution

(1.1)

where

(1.2)

is the standard normal cumulative.

Two time-honored measures of scatter are the mean absolute deviation

(1.3)

and the root mean square deviation

(1.4)

There was a dispute between Eddington (1914, p. 147) and Fisher (1920, footnote on p. 762) about the relative merits of d_n and s_n. Eddington had advocated the use of the former: “This is contrary to the advice of most textbooks; but it can be shown to be true.” Fisher seemingly settled the matter by pointing out that for identically distributed normal observations s_n is about 12% more efficient than d_n.

Of course, the two statistics measure different characteristics of the error distribution. For instance, if the errors are exactly normal, s_n converges to σ, while d_n converges to

So we must be precise about how their performances are to be compared; we use the asymptotic relative efficiency (ARE) of d_n relative to s_n, defined as follows:

(1.5)

The results are summarized in Exhibit 1.1.

Exhibit 1.1 Asymptotic efficiency of mean absolute deviation relative to root mean square deviation. From Huber (1977b), with permission of the publisher.

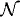
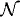
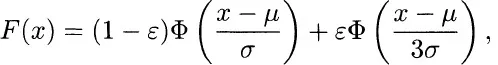
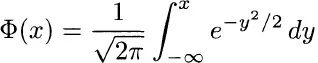
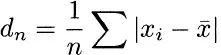
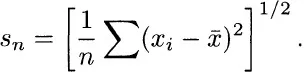
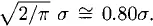
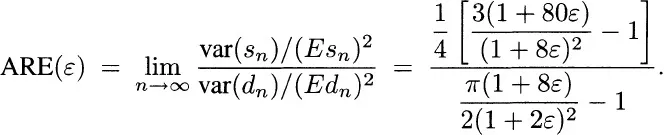
ε	ARE(ε)
0	0.876
0.001	0.948
0.002	1.016
0.005	1.198
0.01	1.439
0.02	1.752
0.05	2.035
0.10	1.903
0.15	1.689
0.25	1.371
0.5	1.017
1.0	0.876

The result is disquieting: just 2 bad observations in 1000 suffice to offset the 12% advantage of the mean square error, and ARE(ε) reaches a maximum value greater than 2 at about ε = 0.05. This is particularly unfortunate since in the physical sciences typical “good data” samples appear to be well modeled by an error law of the form (1.1) with ε in the range between 0.01 and 0.1. (This does not imply that these samples contain between 1% and 10% gross errors, although this is very often true; the above law (1.1) may just be a convenient description of a slightly longer-tailed than normal distribution.) Thus it becomes painfully clear that the naturally occurring deviations from the idealized model are large enough to render meaningless the traditional asymptotic optimal...

Table of contents

• COVER
• TITLE
• COPYRIGHT
• PREFACE
• PREFACE TO FIRST EDITION
• CHAPTER 1: GENERALITIES
• CHAPTER 2: THE WEAK TOPOLOGY AND ITS METRIZATION
• CHAPTER 3: THE BASIC TYPES OF ESTIMATES
• CHAPTER 4: ASYMPTOTIC MINIMAX THEORY FOR ESTIMATING LOCATION
• CHAPTER 5: SCALE ESTIMATES
• CHAPTER 6: MULTIPARAMETER PROBLEMS—IN PARTICULAR JOINT ESTIMATION OF LOCATION AND SCALE
• CHAPTER 7: REGRESSION
• CHAPTER 8: ROBUST COVARIANCE AND CORRELATION MATRICES
• CHAPTER 9: ROBUSTNESS OF DESIGN
• CHAPTER 10: EXACT FINITE SAMPLE RESULTS
• CHAPTER 11: FINITE SAMPLE BREAKDOWN POINT
• CHAPTER 12: INFINITESIMAL ROBUSTNESS
• CHAPTER 13: ROBUST TESTS
• CHAPTER 14: SMALL SAMPLE ASYMPTOTICS
• CHAPTER 15: BAYESIAN ROBUSTNESS
• REFERENCES
• INDEX