Speed Mathematics

Bill Handley

• Publisher: Wiley
• Year: 2012
• Print ISBN: 9780731407811
• eBook ISBN: 9781118302620
• Edition: 3
• Topic: Education
• Subtopic: Teaching Mathematics

This new, revised edition of the bestselling Speed Mathematics features new chapters on memorising numbers and general information, calculating statistics and compound interest, square roots, logarithms and easy trig calculations. Written so anyone can understand, this book teaches simple strategies that will enable readers to make lightning-quick calculations. People who excel at mathematics use better strategies than the rest of us; they are not necessarily more intelligent. With Speed Mathematics you'll discover methods to make maths easy and fun. This book is perfect for students, parents, teachers and anyone who enjoys working with figures and even those who are terrified of numbers!

Chapter 1

Multiplication: Part one

How well do you know your basic multiplication tables?

How would you like to master your tables up to the 10 times tables in less than 10 minutes? And your tables up to the 20 times tables in less than half an hour? You can, using the methods I explain in this book. I only assume you know the 2 times tables reasonably well, and that you can add and subtract simple numbers.

Multiplying numbers up to 10

We will begin by learning how to multiply numbers up to 10 × 10. This is how it works:

We’ll take 7 × 8 as an example.

Write 7 × 8 = down on a piece of paper and draw a circle below each number to be multiplied.

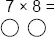
Now go to the first number to be multiplied, 7. How many more do you need to make 10? The answer is 3. Write 3 in the circle below the 7. Now go to the 8. What do we write in the circle below the 8? How many more to make 10? The answer is 2. Write 2 in the circle below the 8.

Your work should look like this:

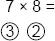
Now subtract diagonally. Take either one of the circled numbers (3 or 2) away from the number, not directly above, but diagonally above, or crossways. In other words, you either take 3 from 8 or 2 from 7. You only subtract one time, so choose the subtraction you find easier. Either way, the answer is the same, 5. This is the first digit of your answer.

8 − 3 = 5 or 7 − 2 = 5

Now multiply the numbers in the circles. Three times 2 is 6. This is the last digit of your answer. The answer is 56. This is how the completed problem looks.

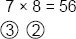
If you know the 2 times tables reasonably well, you can easily master the tables up to the 10 times table, and beyond. Let’s try another example, 8 × 9.

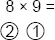
How many more to make 10? The answer is 2 and 1. We write 2 and 1 in the circles below the numbers. What do we do now? We subtract diagonally.

8 − 1 = 7 or 9 − 2 = 7

Seven is the first digit of your answer. Write it down. Now multiply the two circled numbers.

2 × 1 = 2

Two is the last digit of the answer. The answer is 72.

Isn’t that easy? Here are some problems to try by yourself. Instead of writing the answers in the book, you may prefer to write the answers on a piece of paper or in an exercise book so that you can do the problems again if you wish.

a) 9 × 9 =

b) 8 × 8 =

c) 7 × 7 =

d) 7 × 9 =

e) 8 × 9 =

f) 9 × 6 =

g) 5 × 9 =

h) 8 × 7 =

Do all of the problems, even if you know your tables well. This is the basic strategy we will use for almost all of our multiplication.

How did you go? The answers are:

a) 81

b) 64

c) 49

d) 63

e) 72

f) 54

g) 45

h) 56

Isn’t this the easiest way to learn your tables?

To learn or not to learn tables?

Now that you have mastered this method, does it mean you don’t have to learn your tables?

The answer is yes and no.

No, you don’t have to memorise your tables because you can now, with a little practice, calculate your tables instantly. If you already know your tables then learning this method is a bonus.

The good news is that, if you don’t know them, you will learn your tables in record time. After you have calculated 7 × 8 = 56 a dozen or more times you will find you remember the answer. In other words, you have learnt your tables. Again, this is the easiest method I know to learn your tables, and the most pleasant. And you don’t have to worry if you haven’t learnt them all by heart — you will calculate the answers so quickly that everyone will believe you know them anyway.

Multiplying numbers greater than 10

Does this method work for multiplying large numbers?

It certainly does. Let’s try an example:

96 × 97 =

What do we take these numbers up to? How many more to make what? One hundred. So we write 4 under 96 and 3 under 97.

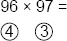
What do we do now? We take away diagonally. 96 minus 3 or 97 minus 4 equals 93. This is the first part of your answer. What do we do next? Multiply the numbers in the circles. Four times 3 equals 12. This is the last part of the answer. The full answer is 9312.

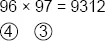
Which method is easier, this method or the method you learned in school? This method, definitely.

Remember my first law of mathematics:

The easier the method you use, the faster you do the problem and the less likely you are to make a mistake.

Now, here are some more problems to do by yourself.

a) 96 × 96 =

b) 97 × 95 =

c) 95 × 95 =

d) 98 × 95 =

e) 98 × 94 =

f) 97 × 94 =

g) 98 × 92 =

h) 97 × 93 =

The answers are:

a) 9216

b) 9215

c) 9025

d) 9310

e) 9212

f) 9118

g) 9016

h) 9021

...

Table of contents

• Cover
• Contents
• Title
• Dedication
• Copyright
• Preface
• Introduction
• Chapter 1: Multiplication: Part one
• Chapter 2: Using a reference number
• Chapter 3: Multiplying numbers above and below the reference number
• Chapter 4: Checking answers: Part one
• Chapter 5: Multiplication: Part two
• Chapter 6: Multiplying decimals
• Chapter 7: Multiplying using two reference numbers
• Chapter 8: Addition
• Chapter 9: Subtraction
• Chapter 10: Squaring numbers
• Chapter 11: Short division
• Chapter 12: Long division by factors
• Chapter 13: Standard long division
• Chapter 14: Direct division
• Chapter 15: Division by addition
• Chapter 16: Checking answers: Part two
• Chapter 17: Estimating square roots
• Chapter 18: Calculating square roots
• Chapter 19: Fun shortcuts
• Chapter 20: Adding and subtracting fractions
• Chapter 21: Multiplying and dividing fractions
• Chapter 22: Direct multiplication
• Chapter 23: Estimating answers
• Chapter 24: Estimating hypotenuse
• Chapter 25: Memorising numbers
• Chapter 26: Phonetic pegs
• Chapter 27: Memorising long numbers
• Chapter 28: Logarithms
• Chapter 29: Using what you have learned
• Afterword
• Appendix A: Frequently asked questions
• Appendix B: Estimating cube roots
• Appendix C: Finding any root of a number
• Appendix D: Checks for divisibility
• Appendix E: Why our methods work
• Appendix F: Casting out nines — why it works
• Appendix G: Squaring feet and inches
• Appendix H: How do you get students to enjoy mathematics?
• Appendix I: Solving problems
• Glossary
• Index