Wave Propagation in Fluids

Models and Numerical Techniques

Vincent Guinot

• Publisher: Wiley-ISTE
• Year: 2013
• Print ISBN: 9781848210363
• eBook ISBN: 9781118623619
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Mechanics

This book presents the physical principles of wave propagation in fluid mechanics and hydraulics. The mathematical techniques that allow the behavior of the waves to be analyzed are presented, along with existing numerical methods for the simulation of wave propagation. Particular attention is paid to discontinuous flows, such as steep fronts and shock waves, and their mathematical treatment. A number of practical examples are taken from various areas fluid mechanics and hydraulics, such as contaminant transport, the motion of immiscible hydrocarbons in aquifers, river flow, pipe transients and gas dynamics. Finite difference methods and finite volume methods are analyzed and applied to practical situations, with particular attention being given to their advantages and disadvantages. Application exercises are given at the end of each chapter, enabling readers to test their understanding of the subject.

Chapter 1

Scalar Hyperbolic Conservation Laws in One Dimension of Space

1.1. Definitions

1.1.1. Hyperbolic scalar conservation laws

A one-dimensional hyperbolic scalar conservation law is a Partial Differential Equation (PDE) that can be written in the form

[1.1]

where t and x are respectively the time- and space-coordinates, U is the so-called conserved variable, F is the flux and S is the source term. Equation [1.1] is said to be the conservation form of the conservation law. The following definitions are used:

– The flux F is the amount of U that passes at the abscissa x per unit time due to the fact that U (also called the transported variable) is being displaced.

– The source term S is the amount of U that appears per unit time and per unit volume, irrespective of the amount transported via the flux F. If U represents the concentration in a given chemical substance, the source term may express degradation phenomena, or radioactive decay. S is positive when the conserved variable appears in the domain, and is negative if U disappears from the domain.

– The conservation law is said to be scalar because it deals with only one dependent variable. When several equations in the form [1.1] are satisfied simultaneously, the term “system of conservation laws” is used. Systems of conservation laws are dealt with in Chapter 2.

Only hyperbolic conservation laws are dealt with in what follows. The conservation law is said to be hyperbolic if the flux F is a function of U (and none of its derivatives) and, possibly, of x and t. Such a dependence is expressed in the form

[1.2]

The function F(U, x, t) is called the “flux function”.

NOTE.– The expression F(U, x, t) in equation [1.2] indicates that F depends on U at the abscissa x at the time t and does not depend on such quantities as derivatives of U with respect to time or space. For instance, the following expression

[1.3]

is a permissible expression [1.2] for F, while the following diffusion flux,

[1.4]

where D is the diffusion coefficient, does not yield a hyperbolic conservation law because the flux F is a function of the first-order derivative of U with respect to space.

In the case of a zero source term, equation [1.1] becomes

[1.5]

In such a case (see section 1.1.2), U is neither created nor destroyed over the domain. The total amount of U over the domain varies only due to the difference between the incoming and outgoing fluxes at the boundaries of the domain.

Depending on the expression of the flux function, the conservation law is said to be convex, concave or non-convex (Figure 1.1):

– The law is convex when the second-order derivative ∂2F/∂U 2 of the flux function with respect to U is positive for all U.

– The law is concave when the second-order derivative ∂2F/∂...

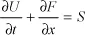
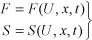
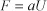
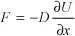
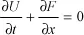
Table of contents

• Cover
• Title Page
• Copyright
• Introduction
• Chapter 1: Scalar Hyperbolic Conservation Laws in One Dimension of Space
• Chapter 2: Hyperbolic Systems of Conservation Laws in One Dimension of Space
• Chapter 3: Weak Solutions and their Properties
• Chapter 4: The Riemann Problem
• Chapter 5: Multidimensional Hyperbolic Systems
• Chapter 6: Finite Difference Methods for Hyperbolic Systems
• Chapter 7: Finite Volume Methods for Hyperbolic Systems
• Appendix A: Linear Algebra
• Appendix B: Numerical Analysis
• Appendix C: Approximate Riemann Solvers
• Appendix D: Summary of the Formulae
• References
• Index