Maths from Scratch for Biologists

Alan J. Cann

• Publisher: Wiley
• Year: 2013
• Print ISBN: 9780471498353, 9780471498346
• eBook ISBN: 9781118685709
• Edition: 1
• Topic: Biowissenschaften
• Subtopic: Biologie

Numerical ability is an essential skill for everyone studying the biological sciences but many students are frightened by the 'perceived' difficulty of mathematics, and are nervous about applying mathematical skills in their chosen field of study. Having taught introductory maths and statistics for many years, Alan Cann understands these challenges and just how invaluable an accessible, confidence building textbook could be to the fearful student. Unable to find a book pitched at the right level, that concentrated on why numerical skills are useful to biologists, he wrote his own. The result is Maths from Scratch for Biologists , a highly instructive, informal text that explains step by step how and why you need to tackle maths within the biological sciences.

Features:

* An accessible, jargon-busting approach to help readers master basic mathematical, statistical and data handling techniques in biology
* Numerous end of chapter problems to reinforce key concepts and encourage students to test their newly acquired skills through practise
* A handy, time-saving glossary
* A supplementary website with numerous problems and self-test exercises

1

Maths in Biology

Mathematics, from the Greek, manthano, ‘to learn’

Some people opt to undertake studies in biology in the belief (conscious or unconscious) that this is a way of pursuing a scientific career while avoiding maths. This book is designed to be accessible to students who, with or without formal mathematical qualifications, are frightened by the perceived ‘difficulty’ of maths and hence are unwilling to apply what mathematical skills they might have. Have you ever noticed when you have been taught how to solve a mathematical problem, that you still don’t know why you need to do a particular step? This is the root of many problems with maths, so this book will try explain the why of maths, in addition to the how. Sometimes, these explanations may seem unnecessary, but I urge you not to skip them – understanding why you need to do something is the key to remembering how to do it. The intention is to be informal and confidence-building to ensure that all readers will gain a general appreciation of basic mathematical, statistical and data handling techniques appropriate to biology. I will try to explain the jargon which confuses the non-numerically minded.

In subsequent chapters, we will look at manipulating numbers, units and conversions, molarities and dilutions, areas and volumes, exponents and logs and statistics. However, the basic advice in this chapter is really the most important part of the book, so please keep reading.

1.1. What can go wrong?

It is easy to make mistakes with maths. One answer looks much like another, so how can you tell if it is right or not? Look at some examples of the sort of mistakes it is all too easy to make. Everyone knows that numbers are meaningless without the units which define what they mean (more of this in Chapter 3). Even if we avoid the elementary mistake of forgetting this and giving an answer of ‘33.6’ (33.6 what? volts? metres? frogs?), things are not always simple. Consider the following questions:

An aquarium has internal dimensions of 100 * 45 * 45 cm. What is its volume in litres?

This is fairly simple. Calculate the volume in cubic centimetres then convert to litres. 1 litre = 1000 cm³ so divide by 1000:

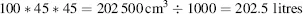
However, life is not always that simple. If the same calculation is given in a different way, it is not as easy to answer:

An aquarium has internal dimensions of 39 * 18 * 18 inches. What is its volume in litres?

This is harder because the units in which the data is given and those in which the answer is required are from different systems of measurement. In real life, this happens all too frequently.

WARNING!

Using mixed units is dangerous (see Chapter 3).

To avoid mistakes we need to convert the units so that they are consistent throughout. However, this means there are two ways to do the calculation:

1. Convert inches to centimetres (1 inch = 2.54 cm), then perform the calculation as above,

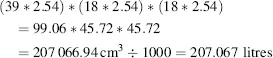
2. Calculate the volume in cubic inches, then convert to litres (1 cubic inch = 0.0164 litres, so conversion factor = 0.0164):

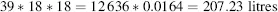
In general, the best method is the one which requires fewer conversions and fewer steps (b). However, this depends on what conversion factors you have to hand – if you have to calculate a conversion factor from cubic inches to litres, it may be better to use (a). Note that the accuracy of conversions from one unit to another depends on the number of significant figures used. Significant figures are: ‘the minimum number of digits needed to write a given value (in scientific notation) without loss of accuracy’. The most significant figure is the left-most digit, the digit which is known most precisely. The least significant figure is the right-most digit, the digit which is known least precisely.

Significant figures are important when reporting scientific data because they give the reader an idea of how accurately data has been measured. Here are the rules:

1. All non-zero numbers (1, 2, 3, 4, 5, 6, 7, 8, 9) are always significant, e.g. 12 345 has five significant figures; 1.2345 also has five significant figures.

2. All zeroes between non-zero numbers are always significant, e.g. 10 002 has five significant figures; 1.0002 also has five significant figures.

3. All zeroes which are to the right of the decimal point and at the end of the number are always significant. This rule sometimes confuses people since they cannot understand why. The reason is because these zeros determine the accuracy to which the number has been calculated, e.g. 1.2001 has five significant figures; 12 000 has two significant figures; 1.0200 has five significant figures (here the ‘placeholder’ zero to the right of the decimal point is significant because it is between non-zero numbers).

4. All other zeroes are not significant numbers, e.g. 1 000 000 has one significant figure (the zeros are just ‘placeholders’); 1 000 000.00 has three significant figures (the 1 and the two zeros at the end of the number); 0.0200 has three significant figures (the ‘placeholder’ zero to the right of the decimal point is not significant since it is not between non-zero numbers); 1 000 000.01 has nine significant figures (zeros between non-zero numbers).

Using the appropriate number of significant figures in calculations is important, since it prevents loss of accuracy. However, computers and calculators frequently give ridiculously large numbers of significant figures – way beyond the accuracy with which a measurement could be made. For this reason, and for ease of performing calculations (particularly when estimating, see below), it is often necessary to ‘round off’ the number of significant figures in a number. Note that this is ‘rounding off’, not ‘rounding up’, which leads to inaccuracy and errors. ‘Rounding up’ a digit which is followed by a 5 (e.g. 5.45 becomes 5.5) introduces errors in calculations because the digits one, two, three and four are ‘rounded down’ (four possibilities) but the digits five, six, seven, eight and nine are all ‘rounded up’ (five possibilities). ‘Rounding off’ avoids this error:

1. If the digit following the figure that is to be the last digit is less than 5, drop it and all the figures to the right of it.

2. If the digit following the figure that is to be the last digit is more than 5, increase by 1 the digit to be rounded, i.e. the preceding figure.

3. If the digit following the figure that is to be the last digit is 5, round the preceding figure so that it is even.

Examples

Round 123.456789 to three significant figures = 123 (rule a: round the number off)

Round 123.456789 to five significant figures = 123.46 (rule b: round the last digit up)

Round 123.456789 to four significant figures = 123.4 (rule c: make the last digit even)

Round 123.356789 to four significant figures = 123.4 (rule c: make the last digit even)

Round 123.456799 to eight significant figures = 123.45680 (note that 9 rounds up to 10, not down to 0).

1.2. Estimating

Whenever you have calculated an answer, always make a rough estimate to see if your answer is sensible and to avoid mistakes.

Calculators and computers spit out numbers at the press of a key, but are the answers right? Estimating is a vital skill if you wish to become confident and proficient with numbers. However, estimating and calculating are not the same thing and it is important to understand the difference. Where calculation attempts to produce the most accurate answer possible (within limits of experimental error), estimation deliberately avoids accuracy in order to simplify working out the answer.

1. If the question is 6 * 5 and your calculated answer is 4, could this possibly be correct? Could the answer be less than the numbers multiplied together?

2. If you are asked to solve an equation for x (Chapter 2) and your answer is 7x, something is wrong.

3. When you calculate the answer to 6.42213 ÷ 2.36199 to six significant figures (2.71895), make an estimate to one or two significant figures to check: 6 ÷ 2 = 3, so 2.71895 looks right, whereas 27.1895 looks wrong.

If you have used a computer or calculator to calculate an answer, it is best to work out the estimate in your head or on a scrap of paper in order to check for any errors you may have introduced by using the machine. This is why estimation involves simplifying the calculation – an estimate is not meant to be accurate, but it should be easy to calculate and a reliable check. Aside from performing the calculation, estimating is the most important part of ensuring that answers to problems are correct. Some calculations in biology are complex and involve many steps (Chapter 5). Estimating is particularly important here to ensure the answer looks sensible. Manipulation of numbers and equations may not give a numerical answer but a mathematical term (e.g. 3y – 2). Here, the trick is to check your answer by substituting back into the original equation to see if it works (Chapter 2).

1.3. How to use this book

If you have been told to use this book as part of a particular course, you had better follow the instructions given by whoever is running the course. Other than that, you can use this book however you want. Some people may want to read though all (or most) of the chapters in order. Others may skip sections and dip into chapters that they feel they need. Either way is fine, as long as you can solve problems consistently and accurately and, most importantly, that you gain the knowledge and confidence to start to try to work out possible answers.

1.4. Mathematical conventions used in this book

To make them easier to read, numbers with more than four digits are split into groups of three digits separated by spaces (not commas), e.g. 9 999 999 is nine million, nine hundred and ninety nine thousand, nine hundred and ninety nine. I have also chosen to use the asterisk (*) as a multiplication sign rather than ‘×’ or a dot, since these are sometimes confusing when written.

2

Manipulating Numbers

Algebra (from the Arabic, al-jabr, ‘the reduction’) – a form of maths where symbols are used to represent numbers

LEARNING OBJECTIVES:

On completing this chapter, you should be able to:

• understand the basic rules of algebra;
• perform simple algebraic manipulations;
• identify and manipulate fractions.

Arithmetic is concerned with the effect of operations (e.g. addition, multiplication, etc.) on specified numbers. In algebra, operations are applied to variables rather than specific numbers. Why? Here is a classic example:

John is 10 years old. His father is 35 years old. After how many years will the father be twice as old as the son?

You could try to find the answer by experimenting with different numbers, but this is laborious. The better way is to treat this an algebra problem and write the problem as an equation which we can then solve.

Let the father be twice as old as the son in x years time. The son will then be (10 + x) years old and the father will be (35 + x) year old:

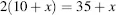
Therefore,

Simplify this by subtracting x from each side to keep the equation balanced:

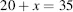
Simplify by subtracting 20 from each side to keep the equation balanced:

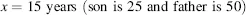
2.1. Manipulating numbers

To manipulate numbers, you need to know the rules. In mathematics, this is known as the ‘Order of Operations’ – an internationally agreed set of arbitrary rules which allows mathematicians the world over to arrive at the same answers to problems:

In algebra, there are two sorts of statement which you need to be able to recognize:

1. A mathematical expression is a string of symbols which describes (‘expresses’) a (potential) calculation using operators (symbols indicating an operation to be performed, e.g. plus, minus, divide, etc.) and operands (symbols which the operators act on), e.g.

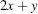
Expressions do not contain an equal sign, but can often be simplified, that is converted to a s...

Table of contents

• Cover
• Contents
• Title Page
• Copyright
• Preface
• 1 Maths in Biology
• 2 Manipulating Numbers
• 3 Units and Conversions
• 4 Molarities and Dilutions
• 5 Areas and Volumes
• 6 Exponents and Logs
• 7 Introduction to Statistics
• 8 Descriptive Statistics
• 9 Probability
• 10 Inferential Statistics
• 11 Correlation and Regression
• Appendix 1 Answers to Problems
• Appendix 2 Software for Biologists
• Appendix 3 Statistical Formulae and Tables
• Appendix 4 Glossary
• Index