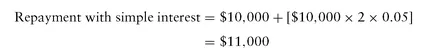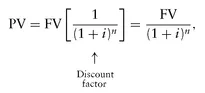Foundations and Applications of the Time Value of Money

Pamela Peterson Drake, Frank J. Fabozzi

• Publisher: Wiley
• Year: 2009
• Print ISBN: 9780470407363
• eBook ISBN: 9780470526026
• Edition: 1
• Topic: Business
• Subtopic: Investimenti e titoli
• Index: Business

Comprehensive coverage of the time value of money

In this book, authors Pamela Peterson Drake and Frank Fabozzi fully expand upon the type of time value of money (TVM) concepts usually presented as part of overviews given in other general finance books. Various TVM concepts and theories are discussed, with the authors offering many examples throughout each chapter that serve to reinforce the tools and techniques covered. Problems and detailed solutions-demonstrated using two different financial calculators, as well as Excel-are also provided at the end of each chapter, while glossary terms are provided in an appendix to familiarize you with basic terms.

• Provides the basic foundations of the time value of money
• Covers issues ranging from an introduction of financial mathematics to calculating present/future values and understanding loan amortization
• Contains problem/solution sets throughout, so you can test your knowledge of the topics discussed

Understanding the time value of money is essential, and this reliable resource will help you gain a firm grasp of its many aspects and its real-world applications.

PART One

The Basics of the Time Value of Money

CHAPTER 1

The Value of Compounding

Remember that time is money.

—Benjamin Franklin
Advice to a Young Tradesman (1748)

Most people are familiar with the Seven Wonders of the World: the Great Pyramid of Giza, the Hanging Gardens of Babylon, the Statue of Zeus at Olympia, the Temple of Artemis at Ephesus, the Mausoleum of Maussollos at Halicarnassus, the Colossus of Rhodes, and the Lighthouse of Alexandria. Supposedly, when Baron von Rothschild was asked if he could list the Seven Wonders, he said he could not. However, he did respond by saying that he could name the Eighth Wonder of the World: compound interest. Actually, labeling compound interest as the Eighth Wonder of the World has been attributed to other notable figures: Benjamin Franklin, Bernard Baruch, and Albert Einstein. Regardless of to whom we attribute this label, as you will see in this chapter, the label is appropriate.

One of the most important tools in personal finance and investing is the time value of money. Evaluating financial transactions requires valuing uncertain future cash flows; that is, determining what uncertain cash flows are worth at different points in time. We are often concerned about what a future cash flow or a set of future cash flows are worth today, though there are applications in which we are concerned about the value of a cash flow at a future point in time.

One complication is the time value of money: a dollar today is not worth a dollar tomorrow or next year. Another complication is that any amount of money promised in the future is uncertain, some riskier than others.

Moving money through time—that is, finding the equivalent value to money at different points in time—involves translating values from one period to another. Translating money from one period involves interest, which is how the time value of money and risk enter into the process.

Interest is the compensation for the opportunity cost of funds and the uncertainty of repayment of the amount borrowed; that is, it represents both the price of time and the price of risk. The price of time is compensation for the opportunity cost of funds—what someone could have done with the money elsewhere—and the price of risk is compensation for bearing risk. That is, the riskier the investment, the higher the interest rate.

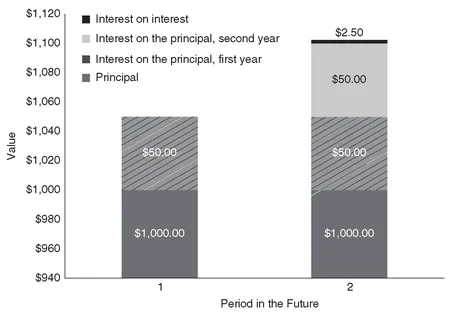
Interest is compound interest if interest is paid on both the principal—the amount borrowed—and any accumulated interest. In other words, if you borrow $1,000 today for two years and the interest is 5% compound interest, at the end of two years you must repay the $1,000, plus interest on the $1,000 for two years and interest on the interest. The amount you repay at the end of two years is $1,102.50:

You can see the accumulation of values in Exhibit 1.1. The $2.50 in the second year is the interest on the first period’s interest.

EXHIBIT 1.1 Components of the Future Value of $1,000 Invested at 5% for Two Years

We refer to translating a value today into a value in the future as compounding , whereas discounting is translating a future value into the present.

The future value is the sum of the present value and interest:

Future value = Present value + Interest

Most financial transactions involve compound interest, though there are a few consumer transactions that use simple interest. Simple interest is the financing arrangement in which the amount repaid is the principal amount and interest on the principal amount. That is, interest is paid only on the principal or amount borrowed. For example, if you borrow $10,000 at 5% simple interest and repay the loan after two years, you must repay the $10,000, plus two periods’ interest at 5%:

In the case of compound interest, the amount repaid has three components:

1. The amount borrowed

2. The interest on the amount borrowed

3. The interest on interest

The basic valuation equation is the foundation of all the financial mathematics that involves compounding, and if you understand this equation, you understand most everything in financial mathematics: where: FV = the future value PV = the present value i = the rate of interest n = is the number of compounding periods

FV = PV(1 + i )ⁿ

The term (1 + i)ⁿ is the compound factor. When you multiply the value today—the present value—by the compound factor, you get the future value.

We can rearrange the basic valuation equation to solve for the present value, PV:

where 1 ÷ (1 + i)ⁿ is the discount factor. When you multiply the value in the future by the discount factor, you get the present value.

In sum,

The focus of this chapter is on compounding—that is, determining a value in the future. We look at discounting in the next chapter.

OF INTEREST

The word interest is from the Latin word intereo, which means “to be lost.” Interest developed from the concept that lending goods or money results in a loss to the lender because he or she did not have the use of the goods or money that is loaned.

In the English language, the word usury is associated with lendin...

Table of contents

• The Frank J. Fabozzi Series
• Title Page
• Copyright Page
• Preface
• About the Authors
• Introduction
• PART One - The Basics of the Time Value of Money
• PART Two - A Few Applications
• APPENDIX A - Using Financial Calculators
• APPENDIX B - Using Spreadsheets in Financial Calculations
• APPENDIX C - Formulas
• APPENDIX D - Glossary
• APPENDIX E - Solutions to End-of-Chapter Problems
• Index