Solid-State Physics for Electronics

Andre Moliton

• Publisher: Wiley-ISTE
• Year: 2013
• ISBN:
  9781118623244
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Condensed Matter

Describing the fundamental physical properties of materials used in electronics, the thorough coverage of this book will facilitate an understanding of the technological processes used in the fabrication of electronic and photonic devices. The book opens with an introduction to the basic applied physics of simple electronic states and energy levels. Silicon and copper, the building blocks for many electronic devices, are used as examples. Next, more advanced theories are developed to better account for the electronic and optical behavior of ordered materials, such as diamond, and disordered materials, such as amorphous silicon. Finally, the principal quasi-particles (phonons, polarons, excitons, plasmons, and polaritons) that are fundamental to explaining phenomena such as component aging (phonons) and optical performance in terms of yield (excitons) or communication speed (polarons) are discussed.

Chapter 1

Introduction: Representations of Electron-Lattice Bonds

1.1. Introduction

This book studies the electrical and electronic behavior of semiconductors, insulators and metals with equal consideration. In metals, conduction electrons are naturally more numerous and freer than in a dielectric material, in the sense that they are less localized around a specific atom.

Starting with the dual wave-particle theory, the propagation of a de Broglie wave interacting with the outermost electrons of atoms of a solid is first studied. It is this that confers certain properties on solids, especially in terms of electronic and thermal transport. The most simple potential configuration will be laid out first (Chapter 2). This involves the so-called flat-bottomed well within which free electrons are simply thought of as being imprisoned by potential walls at the extremities of a solid. No account is taken of their interactions with the constituents of the solid. Taking into account the fine interactions of electrons with atoms situated at nodes in a lattice means realizing that the electrons are no more than semi-free, or rather “quasi-free”, within a solid. Their bonding is classed as either “weak” or “strong” depending on the form and the intensity of the interaction of the electrons with the lattice. Using representations of weak and strong bonds in the following chapters, we will deduce the structure of the energy bands on which solid-state electronic physics is based.

1.2. Quantum mechanics: some basics

1.2.1. The wave equation in solids: from Maxwell’s to Schrödinger’s equation via the de Broglie hypothesis

In the theory of wave-particle duality, Louis de Broglie associated the wavelength (λ) with the mass (m) of a body, by making:

[1.1]

For its part, the wave propagation equation for a vacuum (here the solid is thought of as electrons and ions swimming in a vacuum) is written as:

[1.2]

If the wave is monochromatic, as in:

then Δs = ΔAe^−iωt and

(without modifying the result we can interchange a wave with form s = A(x, y, z)e^−iωt = A(x, y, z)e^{i 2πvt}). By introducing

(length of a wave in a vacuum), wave propagation ω equation [1.2] can be written as:

[1.3]

[1.3’]

A particle (an electron for example) with mass denoted m, placed into a time-independent potential energy V(x, y, z), has an energy:

(in common with a wide number of texts on quantum mechanics and solid-state physics, this book will inaccurately call potential the “potential energy” – to be denoted V).

The speed of the particle is thus given by

[1.4]

The de Broglie wave for a frequency

can be represented by the function Ψ (which replaces the s in equation [1.2]):

[1.5]

Accepting with Schrödinger that the function ψ (amplitude of Ψ) can be used in an analogous way to that shown in equation [1.3’], we can use equations [1.1] and [1.4] with the wavelength written as:

[1.6]

so that:

[1.7]

This is the Schrödinger equation that can be used with crystals (where V is periodic) to give well defined solutions for the energy of electrons. As we shall see,

these solutions arise as permitted bands, otherwise termed valence and conduction bands, and forbidden bands (or “gaps” in semiconductors) by electronics specialists.

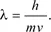
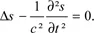
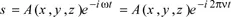
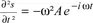
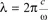
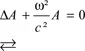
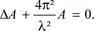
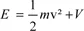
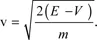
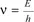
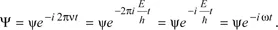
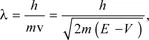
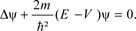
1.2.2. Form of progressive and stationary wave functions for an electron with known energy (E)

In general terms, the form (and a point defined by a vector

) function for an electron of known energy (E) is given by: of a wave

where ψ(

) is the wave function at amplitudes which are in accordance with Schrödinger’s equat...

Table of contents

• Cover
• Titlepage
• Copyright
• Foreword
• Introduction
• Chapter 1: Introduction: Representations of Electron-Lattice Bonds
• Chapter 2: The Free Electron and State Density Functions
• Chapter 3: The Origin of Band Structures within the Weak Band Approximation
• Chapter 4: Properties of Semi-Free Electrons, Insulators, Semiconductors, Metals and Superlattices
• Chapter 5: Crystalline Structure, Reciprocal Lattices and Brillouin Zones
• Chapter 6: Electronic Properties of Copper and Silicon
• Chapter 7: Strong Bonds in One Dimension
• Chapter 8: Strong Bonds in Three Dimensions: Band Structure of Diamond and Silicon
• Chapter 9: Limits to Classical Band Theory: Amorphous Media
• Chapter 10: The Principal Quasi-Particles in Material Physics
• Bibliography
• Index