Operational Research and Networks

Gerd Finke

• Publisher: Wiley-ISTE
• Year: 2013
• Print ISBN: 9781848210929
• eBook ISBN: 9781118617496
• Edition: 1
• Topic: Technology & Engineering
• Subtopic: Electrical Engineering & Telecommunications
• Index: Technology & Engineering

This book presents the principal concepts of operations research (OR), the tools for the planning support and the management of various types of networks. The term "network" is meant to include physical networks, for instance road and rail networks, as well as logical networks that are used in the planning of complex projects. In this case, the vertices of the network correspond to activities and the connections describe temporal relations.

Chapter 1

Linear Programming ¹

1.1. Fundamental concepts

This chapter concerns the problems whose objective is to optimize a function by respecting constraints. Linear programming, more precisely, studies the cases where the function to optimize (or objective function) and the constraints are expressed linearly. This model, which can seem rather specialized, is in fact very flexible. We will show in this chapter that it allows us to model a great many important applications.

Numerous studies describe linear programming techniques. We cite, not wanting to give a long list, some reference studies in French [CHA 96, MIN 83] and in English [BAZ 90, CHV 83, DAN 63, MUR 85, SAK 83, NEM 88].

We first describe an example that illustrates the allocation of resources: the company Biereco produces two varieties of beer, B₁ and B₂, from three ingredients: corn, hops and malt. These cereals are available in quantities of 80, 30 and 40 parts. Each barrel of beer B₁ uses one part corn, one part hops and two parts malt, while each barrel of B₂ must have two parts corn, one part hops and one part malt. A barrel of B₁ is sold at 50 monetary units and a barrel of B₂ is sold at 40 monetary units. The objective of the producer is to maximize the profit. Table 1.1 gives the data for this problem.

Table 1.1. Data for the Biereco example

We model this problem with the help of a linear program. The decision variables x₁ and x₂ represent the number of barrels of beer B₁ and B₂ to be produced. In order for the solution obtained to be realistic, these variables must be non-negative. The limits on the quantity of available resources and the composition of the beers involve the following constraints:

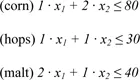
The profit to maximize is given by the function z = 50_x1 + 40_x2. We thus obtain the linear program below:

(objective function) maximize z = 50x₁ + 40x₂

(constraints)	1 x1 + 2 x2 = 80
	1 x1 + 1 x2 = 30
	2 x1 + 1 x2 = 40
	x1 = 0, x2 = 0

The linearity of the objective function and the constraints is natural for this type of problem. In effect, the profits and the consumption of the resources are additives.

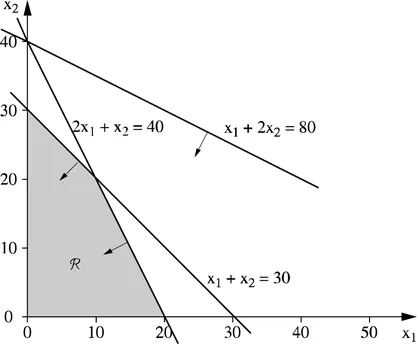
Figure 1.1 describes the set of feasible solutions R: the elements of R satisfy all the constraints. The constraints are inequations. They are thus represented by halfplanes (in the figure, the arrows indicate which half-plane is to be considered). By definition, R is the intersection of these half-planes.

Figure 1.1. Admissible region R

The region R represents the candidates (x₁, x₂) in competition to maximize the objective function. Let us consider the straight lines 50x₁ + 40x₂ = z where z is a constant. On each of these lines, the profit remains the same (Figure 1.2).

The optimal solution to the Biereco problem is x₁ = 10 and x₂ = 20 and the maximum profit is z = 1,300. This example enables us to come to several conclusions:

– The constraint of corn is oversized. In effect, no feasible solution attains the limit of 80 available units.

Figure 1.2. Different values of the objective function

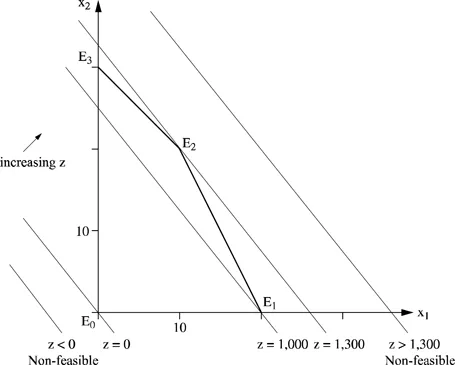
– The extreme points of R, E₀ = (0, 0), E₁ = (20, 0), E₂ = (10, 20) and E₃ = (0, 30) are particularly interesting. In each of these points, at least two constraints are saturated. In this example, E₂ is optimal and it saturates the constraints of hops and malt. The construction of Figure 1.2 shows that each linear objective function admits an optimal solution in an extreme point. This optimal extreme point is not necessarily unique. For example, let us modify the objective: z’ = 60x₁ + 30x₂. In this case, the extreme points E₁ and E₂ are both optimal.

– A point that saturates several constraints simultaneously is not necessarily an extreme point. For example, the point (0.40) saturates the three constraints x₁ ≥ 0, x₁ + 2x₂ ≤ 80 and 2x₁ + x₂ ≤ 40, but is non-feasible. However, when the number of constraints is finite, the...

Table of contents

• Cover
• Title Page
• Copyright
• Introduction
• Chapter 1: Linear Programming
• Chapter 2: Graphs and Networks
• Chapter 3: Classical Combinatorial Problems and Solution Techniques
• Chapter 4: Project Scheduling
• Chapter 5: Operations Management in Transportation Networks
• Chapter 6: Pickup and Delivery Problems with Services on Nodes or Arcs of a Network
• Chapter 7: Telecommunication Networks
• Chapter 8: Mission Planning for Observation Satellites
• List of Authors
• Index