Ant Colony Optimization and Constraint Programming

Christine Solnon

• Publisher: Wiley-ISTE
• Year: 2013
• Print ISBN: 9781848211308
• eBook ISBN: 9781118618899
• Edition: 1
• Topic: Computer Science
• Subtopic: Software Development
• Index: Computer Science

Ant colony optimization is a metaheuristic which has been successfully applied to a wide range of combinatorial optimization problems. The author describes this metaheuristic and studies its efficiency for solving some hard combinatorial problems, with a specific focus on constraint programming. The text is organized into three parts.

The first part introduces constraint programming, which provides high level features to declaratively model problems by means of constraints. It describes the main existing approaches for solving constraint satisfaction problems, including complete tree search approaches and metaheuristics, and shows how they can be integrated within constraint programming languages.

The second part describes the ant colony optimization metaheuristic and illustrates its capabilities on different constraint satisfaction problems.
The third part shows how the ant colony may be integrated within a constraint programming language, thus combining the expressive power of constraint programming languages, to describe problems in a declarative way, and the solving power of ant colony optimization to efficiently solve these problems.

Chapter 1

Introduction

The ability of ant colonies to form paths for carrying food is rather fascinating. When considering the scale of ants, this path-finding problem is complex: ants only have a local perception of their environment, they do not have maps and they do not use GPS. The problem is solved collectively by the whole colony: paths actually emerge from a huge number of elementary interactions.

This collective problem-solving mechanism has given rise to a metaheuristic – that is, a generic approach for solving problems – referred to as ant colony optimization (ACO). The first ACO algorithm was initially proposed by Dorigo in 1992 to solve the traveling salesman problem, the goal of which is to find the shortest tour that passes through a given set of cities. Since this pioneering work, ant colony optimization has been used to solve many complex combinatorial optimization problems.

These combinatorial problems are challenging for computer scientists since solving them may involve the review of a huge number (usually exponential) of combinations. Most people will be familiar with the combinatorial explosion phenomenon, which transforms an apparently simple problem into a tricky brain teaser as soon as the size of the problem to be solved is increased.

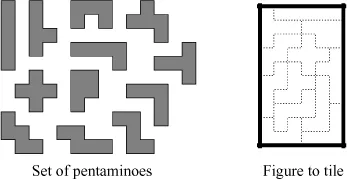
For example, let us consider pentamino puzzles. The goal of such puzzles is to tile a figure with a given set of pentaminoes (shapes composed of five adjacent squares) without overlapping, as illustrated in Figure 1.1.

Figure 1.1. Example of pentamino puzzle; the solution is displayed in dashed lines

When the number of pentaminoes is small enough, these problems are rather easily solved by a systematic review of all possible combinations. However, when the number of pentaminoes is slightly increased, the number of different combinations to review increases so drastically that the problem can no longer be solved by a simple enumeration. For larger problems, even the most powerful computer cannot enumerate all combinations within a reasonable amount of time.

The challenge of solving these problems clearly goes beyond puzzles. This combinatorial explosion phenomenon also occurs in many industrial problems such as scheduling activities, planning a production or packing objects of different volumes into a finite number of bins. It is therefore highly important to design algorithms that are actually able to solve these difficult combinatorial problems.

This book examines the ability of ant colony optimization for solving these complex combinatorial problems. This study is carried out within the context of constraint programming, which allows us to describe combinatorial problems in a declarative way by means of constraints.

1.1. Overview of the book

The book comprises three parts, described in the following sections.

As a preamble to these three parts, we introduce combinatorial problems and discuss computational complexity issues in Chapter 2. The goal is to provide a clear understanding of the challenge: as the combinatorial explosion cannot be avoided, we have to design intelligent approaches which are able to restrain or get around it.

1.1.1. Constraint programming

The first part of this book provides an overview of different existing approaches for solving combinatorial problems within the context of constraint programming.

We introduce constraint satisfaction problems in Chapter 3, which provide a framework for modeling combinatorial problems in a declarative way by means of constraints.

We then describe three main types of approaches that may be used to solve constraint satisfaction problems.

Exact approaches are described in Chapter 4, where we explore the space of combinations in a systematic way until either a solution is found or inconsistency is proven. In order to (try to) restrain combinatorial explosion, these approaches structure the set of all combinations in a tree and use pruning techniques to reduce the search space and ordering heuristics to define the order in which it is explored.

Heuristic approaches get around combinatorial explosion by deliberately ignoring some combinations. We discuss the two main types of heuristic approaches:

– Perturbative heuristic approaches (Chapter 5) build new combinations by modifying existing combinations by applying cross-over and mutation operators for genetic algorithms, applying elementary transformations for local searches or moving with respect to a given velocity for particle swarm optimization.

– Constructive heuristic approaches (Chapter 6) use a stochastic model to generate new combinations in an incremental way. This model is static for greedy (randomized) algorithms. It is dynamic and evolves with respect to previous experience for estimation of distribution algorithms and ant colony optimization.

In Chapter 7 we introduce some constraint programming languages. These languages allow the user to describe a combinatorial problem in a declarative way by means of constraints. This problem can then be solved by embedded solving algorithms such as those described in Chapters 4, 5 and 6.

1.1.2. Ant colony optimization

The second part of this book describes ant colony optimization. As for other heuristic approaches described in Chapters 5 and 6, ant colony optimization only explores part of the space of all combinations and uses (meta-) heuristics to guide the search towards the most promising areas while deliberately ignoring others.

Ant colony optimization borrows its features from the collective behavior of ant colonies and, more particularly, from their collective ability to find the shortest path between two points. We therefore begin the second part in Chapter 8 with a description of mechanisms which allow ant colonies to converge towards the shortest paths. We then describe the Ant System, the first ant-based algorithm introduced by Dorigo in 1992 to solve the traveling salesman problem, and we describe the generic framework of ant colony optimization for solving static combinatorial optimization problems.

Beyond the ant metaphor, we describe the mechanisms which allow artificial ants to converge towards solutions in Chapter 9 and, more particularly, those used to balance diversification and intensification:

– Diversification aims to ensure a good sampling of the search space and therefore reduce the risk of ignoring an area which actually contains a solution. This is mainly ensured by use of a stochastic model to construct new combinations.

– Intensification aims to guide the search towards the best combinations. It is ensured by a reinforcement mechanism which exploits past constructions to progressively bias the stochastic model.

In Chapter 10, we describe some extensions of ACO that have recently been proposed to solve continuous problems (where some variables may be defined over continuous numerical intervals), dynamic problems (where data may change during the solution process) and multi-objective optimization problems (where several objective functions require to be optimized).

We conclude this second part with Chapter 11, where we provide hints for implementing ACO algorithms.

1.1.3. Constraint programming with ant colony optimization

Algorithms based on ant colony optimization have proven to be very effective for solving many combinatorial optimization problems. In this book we focus on their ability to solve constraint satisfaction problems, which constitute a generic class of combinatorial problems.

We first illustrate (Chapter 12) the abilities of ant colonies in the car sequencing problem, a real-world industrial problem that is very often used to evaluate constraint programming languages. This problem involves scheduling cars along an assembly line, while satisfying capacity constraints which ensure that the different work units on the assembly line are not overloaded. We show that ant colony optimization obtains very competitive results for this challenging problem.

We study the abilities of ant colonies to solve generic constraint satisfaction problems, for which we do not have any specific knowledge of the constraints used, in Chapter 13. Again, we show that ant colony optimization is able to resolve complex problems in an efficient manner.

We show how to integrate ant colony optimization into a constraint programming library in Chapter 14. This integration allows us to benefit from existing procedures for modeling, verifying and propagating constraints. The tree-based exploration of the search space, usually employed in constraint programming languages, is however replaced by a stochastic exploration guided by previous experiments using the basic principles of ant colony optimization.

Chapter 15 concludes with details of future research which could be carried out for a better integration of ant colony optimization into a constraint programming language.

Chapter 2

Computational Complexity

A problem is said to be combinatorial if it can be resolved by the review of a finite set of combinations. Most often, this kind of solving process is met with an explosion of the number of combinations to review. This is the case, for example, when a timetable has to be designed. If there are only a few courses to schedule, the number of combinations is rather small and the problem is quickly solved. However, adding a few more courses may result in such an increase of the number of combinati...

Table of contents

• Cover
• Title Page
• Copyright
• Foreword
• Acknowledgements
• Chapter 1: Introduction
• Chapter 2: Computational Complexity
• Part I: Constraint Programming
• Part II: Ant Colony Optimization
• Part III: CP with ACO
• Bibliography
• Index