Optimal Learning

Warren B. Powell, Ilya O. Ryzhov

• Publisher: Wiley
• Year: 2013
• Print ISBN: 9780470596692
• eBook ISBN: 9781118309841
• Edition: 1
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

Learn the science of collecting information to make effective decisions

Everyday decisions are made without the benefit of accurate information. Optimal Learning develops the needed principles for gathering information to make decisions, especially when collecting information is time-consuming and expensive. Designed for readers with an elementary background in probability and statistics, the book presents effective and practical policies illustrated in a wide range of applications, from energy, homeland security, and transportation to engineering, health, and business.

This book covers the fundamental dimensions of a learning problem and presents a simple method for testing and comparing policies for learning. Special attention is given to the knowledge gradient policy and its use with a wide range of belief models, including lookup table and parametric and for online and offline problems. Three sections develop ideas with increasing levels of sophistication:

• Fundamentals explores fundamental topics, including adaptive learning, ranking and selection, the knowledge gradient, and bandit problems
• Extensions and Applications features coverage of linear belief models, subset selection models, scalar function optimization, optimal bidding, and stopping problems
• Advanced Topics explores complex methods including simulation optimization, active learning in mathematical programming, and optimal continuous measurements

Each chapter identifies a specific learning problem, presents the related, practical algorithms for implementation, and concludes with numerous exercises. A related website features additional applications and downloadable software, including MATLAB and the Optimal Learning Calculator, a spreadsheet-based package that provides an introduc­tion to learning and a variety of policies for learning.

CHAPTER 1

THE CHALLENGES OF LEARNING

We are surrounded by situations where we need to make a decision or solve a problem, but where we do not know some or all of the relevant information for the problem perfectly. Will the path recommended by my navigation system get me to my appointment on time? Am I charging the right price for my product, and do I have the best set of features? Will a new material make batteries last longer? Will a molecular compound help reduce a cancer tumor? If I turn my retirement fund over to this investment manager, will I be able to outperform the market? Sometimes the decisions have a simple structure (which investment advisor should I use), while others require complex planning (how do I deploy a team of security agents to assess the safety of a set of food processing plants). Sometimes we have to learn while we are doing (the sales of a book at a particular price), while in other cases we may have a budget to collect information before making a final decision.

There are some decision problems that are hard even if we have access to perfectly accurate information about our environment: planning routes for aircraft and pilots, optimizing the movements of vehicles to pick up and deliver goods, or scheduling machines to finish a set of jobs on time. This is known as deterministic optimization. Then there are other situations where we have to make decisions under uncertainty, but where we assume we know the probability distributions of the uncertain quantities: How do I allocate investments to minimize risk while maintaining a satisfactory return, or how do I optimize the storage of energy given uncertainties about demands from consumers? This is known as stochastic optimization.

In this book, we introduce problems where the probability distributions themselves are unknown, but where we have the opportunity to collect new information to improve our understanding of what they are. We are primarily interested in problems where the cost of the information is considered “significant,” which is to say that we are willing to spend some time thinking about how to collect the information in an effective way. What this means, however, is highly problem-dependent. We are willing to spend quite a bit before we drill a $10 million hole hoping to find oil, but we may be willing to invest only a small effort before determining the next measurement inside a search algorithm running on a computer.

The modeling of learning problems, which might be described as “learning how to learn,” can be fairly difficult. While expectations are at least well-defined for stochastic optimization problems, they take on subtle interpretations when we are actively changing the underlying probability distributions. For this reason, we tend to work on what might otherwise look like very simple problems. Fortunately, there are very many “simple problems” which would be trivial if we only knew the values of all the parameters, but which pose unexpected challenges when we lack information.

1.1 LEARNING THE BEST PATH

Consider the problem of finding the fastest way to get from your new apartment to your new job in Manhattan. We can find a set of routes from the Internet or from our GPS device, but we do not know anything about traffic congestion or subway delays. The only way we can get data to estimate actual delays on a path is to travel the path. We wish to devise a strategy that governs how we choose paths so that we strike a balance between experimenting with new paths and getting to work on time every day.

Assume that our network is as depicted in Figure 1.1. Let p be a specific path, and let x_p = 1 if we choose to take path p. After we traverse the path, we observe a cost

. Let μ_p denote the true mean value of

, which is of course unknown to us. After n trials, we can compute a sample mean

of the cost of traversing path p along with a sample variance

using our observations of path p. Of course, we only observe path p if

so we might compute these statistics using

(1.1)

(1.2)

(1.3)

Figure 1.1 A simple shortest path problem, giving the current estimate of the mean and standard deviation (of the estimate) for each path.

Note that

is our estimate of the variance of

by iteration n (assuming we have visited path p

times). The variance of our estimate of the mean,

is given by

Now we face the challenge: Which path should we try? Let’s start by assuming that you just started a new job and you have been to the Internet to find different paths, but you have not tried any of them. If your job involves commuting from a New Jersey suburb into Manhattan, you have a mixture of options that include driving (various routes) and commuter train, with different transit options once you arrive in Manhattan. But you do have an idea of the length of each path, and you may have heard some stories about delays through the tunnel into Manhattan, as well as a few stories about delayed trains. From this, you construct a rough estimate of the travel time on each path, and we are going to assume that you have at least a rough idea of how far off these estimates may be. We denote these initial estimates using

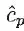
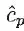
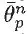
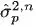
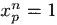
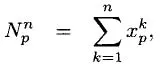
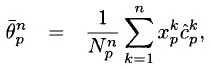
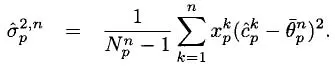
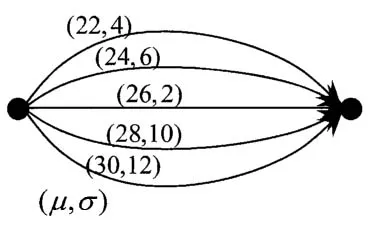
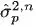
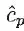
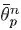
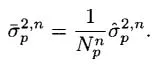
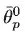	=	initial estimate of the expected travel time on path p,
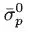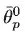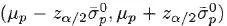
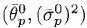
	=	initial estimate of the standard deviation of the difference between and the truth.

If we believe that our estimation errors are normally distributed, then we think that the true mean, μ_p, is in the interval

α percent of the time. If we assume that our errors are normally distributed, we would say that we have an estimate of μ_p that is normally distributed with parameters

.

So which path do you try first? If our priors are as shown in Figure 1.1, presumably we would go with the first path, since it has a mean path time of 22 minutes, which is less than any of the other paths. But our standard deviation around this belief is 4, which means we believe this could possibly be as high as 30. At the same time, there are paths with times of 28 and 30 with standard deviations of 10 and 12. This means that we believe that these paths could have times that are even smaller than 20. Do we always go with the path that we think is the shortest? Or do we try paths that we think are longer, but where we are just not sure, and there is a chance that these paths may actually be better?

If we choose a path we think is best, we say that we are exploiting the information we have. If we try a path because it might be better, which would help us make better decisions in the future, we say that we are exploring. Exploring a new path, we may find that it is an unexpectedly superior option, but it is also possible that we will simply confirm what we already believed. We may even obtain misleading results – it may be that this one route was experiencing unusual delays on the one day we happened to choose it. Nonetheless, it is often desirable to try something new to avoid becoming stuck on a suboptimal solution just because it “seems” good. Balancing the desire to explore versus exploit is referred to in some communities as the exploration versus exploitation problem. Another name is the learn versus earn problem. Regardless of the name, the point is the lack of information when we make a decision, along with the value of new information in improving future decisions.

1.2 AREAS OF APPLICATION

The diversity of problems where we have to address information acquisition and learning is tremendous. Below, we try to provide a hint of the diversity.

Transportation

• Responding to disruptions - Imagine that there has been a disruption to a network (such as a bridge failure) forcing people to go through a process of discovering new travel routes. This problem is typically complicated by noisy observations and by travel delays that depend not just on the path but also on the time of departure. People have to evaluate paths by actually traveling them.
• Revenue management - Providers of transportation need to set a price that maximizes revenue (or profit), but since demand functions are unknown, it is often necessary to do a certain amount of trial and error.
• Evaluating airline passengers or cargo for dangerous items - Examining people or cargo to evaluate risk can be time-consuming. There are different policies that can be used to determine who/what should be subjected to varying degrees of examination. Finding the best policy requires testing them in field settings.
• Finding the best heuristic to solve a difficult integer program for routing and scheduling - We may want to find the best set of parameters to use our tabu search heuristic, or perhaps we want to compare tabu search, genetic algorithms, and integer programming for a particular problem. We have to loop over different algorithms (or variations of an algorithm) to find the one that works the best on a particular dataset.
• Finding the best business rules - A transportation company needs to determine the best terms for serving customers, the best mix of aircraft, and the right pilots to hire¹ (see Figure 1.2). They may use a computer simulator to evaluate these options, requiring time-consuming simulations to be run to evaluate different strategies.
• Evaluating schedule disruptions - Some customers may unexpectedly ask us to deliver their cargo at a different time, or to a different location than what was originally agreed upon. Such disruptions come at a cost to us, because we may need to make significant changes to our routes and schedules. However, the customers may be willing to pay extra money for the disruption. We have a limited time to find the disruption or combination of disruptions where we can make the most profit.

Figure 1.2 The operations center for NetJets®, which manages over 750 aircraft¹. NetJets® has to test different policies to strike the right balance of costs and service.

Energy and the Environment

• Finding locations for wind farms - Wind conditions can depend on microgeography - a cliff, a local valley, a body of water. It is necessary to send teams with sensors to find the best locations for locating wind turbines in a geographical area. The problem is complicated by variations in wind, making it necessary to visit a location multiple times.
• Finding the best material for a solar panel - It is necessary to test large numbers of molecular compounds to find new materials for converting sunlight to electricity. Testing and evaluating materials is time consuming and very expensive, and there are large numbers of molecular combinations that can be tested.
• Tuning parameters for a fuel cell - There are a number of design parameters that have to be chosen to get the best results from a full cell: the power density of the anode or cathode, the conductivity of bipolar plates, and the stability of the seal.
• Finding the best energy-saving technologies for a building - Insulation, tinted windows, motion sensors and automated thermostats interact in a way that is unique to each building. It is necessary to test different combinations to determine the technologies that work the best.
• R&D strategies - There are a vast number of research efforts being devoted to competing technologies (materials for solar panels, biomass fuels, wind turbine designs) which represent projects to collect information about the potential for different designs for solving a particular problem. We have to solve these engineering problems as quickly as possible, but testing different engineering designs is time-consuming and expensive.
• Optimizing the best policy for storing energy in a battery - A policy is defined by one or more parameters that determine how much energy is stored and in what type of storage device. One example might be, “charge the battery when the spot price of energy drops below x.” We can collect information in the field or a computer simulation that evaluates the performance of a policy over a period of time.
• Learning how lake pollution due to fertilizer run-off responds to farm policies - We can introduce new policies that encourage or discourage the use of fertilizer, but we do not fully understand the relationship between these policies and lake pollution, and these policies impose different costs on the farmers. We need to test different policies to learn their impact, but each test requires a year to run and there is some uncertainty in evaluating the results.
• On a larger scale, we need to identify the best policies for controlling CO² emissions, striking a balance between the cost of these policies (tax incentives on renewables, a carbon tax, research and development costs in new technologies) and the impact on global warming, but we do not know the exact relationship between atmospheric CO² and global temperatures.

Figure 1.3 Wind turbines ...

Table of contents

• Cover
• Contents
• Title Page
• Copyright
• Dedication
• PREFACE
• ACKNOWLEDGMENTS
• CHAPTER 1: THE CHALLENGES OF LEARNING
• CHAPTER 2: ADAPTIVE LEARNING
• CHAPTER 3: THE ECONOMICS OF INFORMATION
• CHAPTER 4: RANKING AND SELECTION
• CHAPTER 5: THE KNOWLEDGE GRADIENT
• CHAPTER 6: BANDIT PROBLEMS
• CHAPTER 7: ELEMENTS OF A LEARNING PROBLEM
• CHAPTER 8: LINEAR BELIEF MODELS
• CHAPTER 9: SUBSET SELECTION PROBLEMS
• CHAPTER 10: OPTIMIZING A SCALAR FUNCTION
• CHAPTER 11: OPTIMAL BIDDING
• CHAPTER 12: STOPPING PROBLEMS
• CHAPTER 13: ACTIVE LEARNING IN STATISTICS
• CHAPTER 14: SIMULATION OPTIMIZATION
• CHAPTER 15: LEARNING IN MATHEMATICAL PROGRAMMING
• CHAPTER 16: OPTIMIZING OVER CONTINUOUS MEASUREMENTS
• CHAPTER 17: LEARNING WITH A PHYSICAL STATE
• BIBLIOGRAPHY
• INDEX
• WILEY SERIES IN PROBABILITY AND STATISTICS