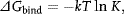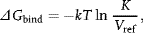Protein-Ligand Interactions

Holger Gohlke, Raimund Mannhold, Hugo Kubinyi, Gerd Folkers

• Publisher: Wiley-VCH
• Year: 2012
• Print ISBN:
  9783527329663
• eBook ISBN:
  9783527645961
• Edition: 1
• Topic: Medizin
• Subtopic: Pharmakologie

Innovative and forward-looking, this volume focuses on recent achievements in this rapidly progressing field and looks at future potential for
development.
The first part provides a basic understanding of the factors governing protein-ligand interactions, followed by a comparison of key experimental methods (calorimetry, surface plasmon resonance, NMR) used in generating interaction data. The second half of the book is devoted to insilico methods of modeling and predicting molecular recognition and binding, ranging from first principles-based to approximate ones. Here,
as elsewhere in the book, emphasis is placed on novel approaches and recent improvements to established methods. The final part looks at
unresolved challenges, and the strategies to address them.
With the content relevant for all drug classes and therapeutic fields, this is an inspiring and often-consulted guide to the complexity of
protein-ligand interaction modeling and analysis for both novices and experts.

Part I

Binding Thermodynamics

Chapter 1

Statistical Thermodynamics of Binding and Molecular Recognition Models

Kim A. Sharp

1.1 Introductory Remarks

Equilibrium binding or association of two molecules to form a bimolecular complex, A + B

AB, is a thermodynamic event. This chapter will cover some of the fundamental thermodynamics and statistical mechanics aspects of this event. The aim is to introduce general principles and broad theoretical approaches to the calculation of binding constants, while later chapters will provide examples. Only the noncovalent, bimolecular association under ambient pressure conditions will be considered. However, extension to higher order association involves no additional principles, and extension to high pressure by inclusion of the appropriate pressure–volume work term is straightforward. In terms of the binding reaction above, the association and dissociation constants are defined as K = [AB]/[A][B] and K_D = [A][B]/[AB] respectively, where [] indicates concentration. Either K or K_D is the primary experimental observable measured in binding reactions. K_D is sometimes obtained indirectly by inhibition of binding of a different ligand as a K_i. From a thermodynamic perspective, the information content from K, K_D, and K_i is the same.

1.2 The Binding Constant and Free Energy

To connect the experimental observable K to thermodynamics, one often finds in the literature the relationship

(1.1)

where k is the Boltzmann constant, T is the absolute temperature, and ΔG_bind is the “absolute” or “standard” binding free energy. Several comments are given to avoid misuse of this expression. First, one cannot properly take the logarithm of a quantity with units such as K, so Eq. (1.1) is implicitly

(1.2)

where V_ref is the reference volume in units consistent with the units of concentration in K, that is, 1 l/mol or about 1660 ų/molecule for molarity units. The choice of V_ref is often referred to as the “standard state” problem. Equivalently, one says that ΔG_bind is the free energy change when reactants A and B and the product AB are all at the reference concentration. Second, although the units of concentration used in K are almost always moles/liter, this is entirely a convention, so the actual numerical value for ΔG_bind obtained from Eq. (1.2) is arbitrary. Put another way, any method for calculating the free energy of binding must explicitly account for a particular choice of V_ref before it can meaningfully be compared with experimental values of ΔG_bind obtained using Eq. (1.2). Furthermore, ligand efficiency-type measures, such as ΔG_bind/n where n is the number of heavy atoms in a ligand or the molecular weight of a ligand [1], can change radically with (arbitrary) choice of concentration units. Of course, differences in ΔG_bind can be sensibly compared provided the same reference state concentration is used. Finally, in Eq. (1.2), the free energy actually depends on the ratio of activities of reactants and products, not on concentrations. For neutral ligands and molecules of low charge density at less than micromolar concentrations, the activity and concentration are nearly equal and little error is introduced. However, this is not true for high charge density molecules such as nucleic acids and many of the ligands and proteins that bind to nucleic acids. Here, the activity coefficient can be substantially different from unity even at infinitely low concentration. Indeed, much of the salt dependence of ligand–DNA binding can be treated as an activity coefficient effect [2–4]. The issue of standard state concentrations, the formal relationship between the binding constant and the free energy, and the effect of activity coefficients are all treatable by a consistent statistical mechanical treatment of binding, as described in Section 1.3.

1.3 A Statistical Mechanical Treatment of Binding

Derivation of a general expression for the binding constant follows closely the approach of Luo and Sharp [5], although somewhat different treatments using chemical potentials, which provide the same final result, are given elsewhere [6–8]. It is a statistical mechanical principle that any equilibrium observable can be obtained as an ensemble, or Boltzmann weighted average, of the appropriate quantity. Here, the binding constant K = [AB]/[A][B] is the required observable. Consider a single molecule each of A and B in some volume V (Figure 1.1) and for convenience define a coordinate system centered on B (the target) in a fixed orientation. Over time, the ligand (A) will explore different positions and orientations (poses) relative to B, where r and Ω represent the three position and three orientation coordinates of A with respect to B. Now A and B interact with each other with an energy that depends not only on their relative position (r, Ω) but in general also on the conformations of A, B, and the surrounding solvent. If n_a, n_b, n_s are the number of atoms in A, B, and solvent, then the energy is a function of 3n_a + 3n_b + 3n_s − 6 coordinates. In principle, one could keep all these degrees of freedom explicit. From a practical standpoint, this would be a complicated and expensive function to evaluate. However, one may integrate over the solvent coordinates and the (3n_a − 6) +(3n_b − 6) internal coordinates so that the interaction between A and B for a given (r, Ω) is described by an interaction potential of mean force (pmf) ω(r, Ω). If one defines the pmf between A and B at infinite separation in their equilibrium conformations to be 0, then ω(r, Ω) is the thermodynamic work of bringing A and B from far apart to some mutual pose (r, Ω), accounting for both solvent effects and internal degrees of free...

Table of contents

• Cover
• Series Page
• Title Page
• Copyright
• List of Contributors
• Preface
• A Personal Foreword
• Part I: Binding Thermodynamics
• Part II: Learning from Biophysical Experiments
• Part III: Modeling Protein–Ligand Interactions
• Part IV: Challenges in Molecular Recognition
• Index