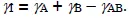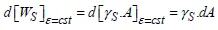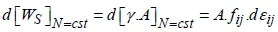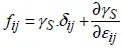Mechanics of Solid Interfaces

Muriel Braccini, Michel Dupeux, Muriel Braccini, Michel Dupeux

• Publisher: Wiley-ISTE
• Year: 2013
• Print ISBN: 9781848213739
• eBook ISBN: 9781118588185
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Mechanics

Mechanics of Solid Interfaces

The growing occurrence of heterogeneous materials such as composites or coated substrates in structural parts makes it necessary for designers and scientists to deal with the specific features of the mechanical behavior of solid interfaces.

This book introduces basic concepts on mechanical problems related to the presence of solid/solid interfaces and their practical applications. The various topics discussed here are the mechanical characterization of interfaces, the initiation and growth of cracks along interfaces, the origin and control of interface adhesion, focusing in particular on thin films on substrate systems. It is designed and structured to provide a solid background in the mechanics of heterogeneous materials to help students in materials science, as well as scientists and engineers.

PART 1

Fundamentals

Chapter 1

Interfaces: the Physics, Chemistry and Mechanics of Heterogeneous Continua

Of what does an interface between two solids consist? What qualifying or quantitative physical or chemical parameters must we specify to define it? What general considerations can we set out about the mechanical behavior of an interface in a heterogeneous solid? These are the basic questions that this chapter proposes to answer as an introduction to the following chapters, focusing on more specific points.

1.1. Definition and terminology

Strictly speaking, an interface can be defined as the two-dimensional border area between two dissimilar materials. These two materials may differ in their physical state (such as in the case of solid–liquid or solid–gas interfaces); their chemical composition (such as an interface between two immiscible liquids in an emulsion); their structure (such as a residual martensite/austenite interface in quenched steel); their relative orientation (such as the twin boundaries or grain boundaries in a polycrystal or the interface between layers in a multilayer composite); or even by their relative translation (such as a stacking fault surface in a crystal). In this book, as the title indicates, we will focus on the case of interfaces between two solid materials.

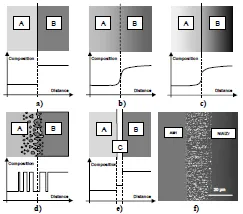
The geometric aspect of a solid–solid interface can prove extremely variable, depending on the scale at which it is observed. Abrupt interfaces, in which the physical and chemical characteristics change suddenly as the interface is crossed (see Figure 1.1a), are an ideal and simple case that is rarely encountered in reality. In real cases, the physical or chemical interaction between the two materials disturbs their composition or their structure in a layer of varying thickness near the interface, producing what we call a diffuse interface, with or without a marked discontinuity of properties (see Figures 1.1b and 1.1c).

Figure 1.1. View and development profile of the physicochemical characteristics (such as chemical composition) across various types of interfaces: a) abrupt interface; b) continuous diffuse interface; c) diffuse interface with discontinuity; d) heterogeneous diffuse interface; e) interface with interphase; and f) real interface between an AM1 nickel-based superalloy and a NiAlZr coating (cross-section, scanning electron microscope (SEM)) [THE 07]

This heterogeneity may even appear as a complex interpenetration of particles or protrusions of adjacent materials (see Figure 1.1d). Finally, the interface may have one or more intermediate layers, or interphases, composed of material that is different from the join between two bulk materials that have either been inserted voluntarily during the development of a synthesis interface (for example, a layer of adhesive in a glued interface) or are the result of a solid state reaction between the two basic materials (see Figure 1.1e and Chapter 5).

Even without taking a closer look at the crystalline or atomic scale (see Chapter 2), it is clear that a real interface almost always has some “thickness”; the ideal notion of an interface reduced to a surface of abrupt separation between two solid media, such as the one in Figure 1.1a, is in reality only a convenient, simplified assumption that is frequently used, keeping in mind that it is only valid on a scale of sufficient width.

1.2. Energy considerations

On the free surface of a solid, or along an internal interface, the interaction stresses acting on an atom or molecule due to its bonds with its neighbors are obviously different from the ones in the bulk of the same solid; since the local atomic environment is neither homogeneous nor isotropic, the result of these interactions is not zero and leads, for example, to atomic reconstructions on the surface or to interatomic distances with equilibrium values that are different from those in the bulk of the material. The same is true for electronic distributions. In the case of the free surface of a homogeneous solid, the result is an increase in internal energy γs in the free surface area (in J/m²) in comparison with any surface embedded within the volume of the solid. This surface energy γ includes an enthalpy contribution due to the local chemical composition, which is different from that within the solid, and an entropy contribution related to the difference in atomic structure between the surface and the volume of the solid. In the case of an interface between two media A and B, for similar reasons each unit of area of the interface represents additional internal energy γ_I, the value of which can be expressed by the Dupré relation (see Chapter 5):

[1.1]

where γ_A and γB are the energies of the surfaces of materials A and B when they are free and γ_AB represents the energy of the interatomic bonds per unit of interface area established between the two materials at the moment when the interface is produced. This energy is usually negative (with the usual conventions of thermodynamics); that is, the side-by-side placement of the two free surfaces leads to a reduction in internal energy, and the interface thus created is more stable than the two separate elements. Its value, on the basis of both theoretical considerations and experimental results, in typically on the order of 1 J/m².

Returning to the case of the total free area of a solid, where the formulation of a physical demonstration is simpler, two different types of variations can be imagined for its total energy, Ws:

– with the extent of area A of the free surface of interest, at constant interatomic distances (the strain ε being constant) we have:

[1.2]

which leads to the definition of the surface energy γs mentioned above;

– with the extent of area A, but at a constant number of atomic sites, N, for variable strains εij (i, j = 1, 2) in the plane (x₁, x₂) of the surface, we have:

[1.3]

which leads to the definition of a second-order, two-dimensional tensor ƒ_ij, the elements of which have the dimension of stresses, called surface stresses. Writing the differential of the previous total energy (equation [1.3]) as d(γ.A) = γ.dA + A.dγ and expressing the variation of area A (at a constant number of sites) as dA = A.δ_ij.ε_ij (i, j = 1, 2, and δ_ij being the Kronecker symbol), we get the expression of the surface stresses in relation to the surface energy γsand its derivative with regard to the strains of the surface plane:

[1.4]

The variations dε_ij of the surface strains are, i...

Table of contents

• Cover
• Title Page
• Copyright
• Foreword
• Part 1: Fundamentals
• Part 2: Singularities, Notches and Interfacial Cracks
• Part 3: Practical Applications
• Part 4: Thin Films
• List of Authors
• Index