Streamlining Digital Signal Processing

A Tricks of the Trade Guidebook

Richard G. Lyons

• Publisher: Wiley-IEEE Press
• Year: 2012
• Print ISBN: 9781118278383
• eBook ISBN: 9781118316931
• Edition: 2
• Topic: Technology & Engineering
• Subtopic: Electrical Engineering & Telecommunications
• Index: Technology & Engineering

This book presents recent advances in DSP to simplify, or increase the computational speed of, common signal processing operations. The topics describe clever DSP tricks of the trade not covered in conventional DSP textbooks. This material is practical, real-world, DSP tips and tricks as opposed to the traditional highly-specialized, math-intensive, research subjects directed at industry researchers and university professors. This book goes well beyond the standard DSP fundamentals textbook and presents new, but tried-and-true, clever implementations of digital filter design, spectrum analysis, signal generation, high-speed function approximation, and various other DSP functions.

Part One
Efficient Digital Filters

Chapter 1

Lost Knowledge Refound: Sharpened FIR Filters

Matthew Donadio

Night Kitchen Interactive

What would you do in the following situation? Let’s say you are diagnosing a DSP system problem in the field. You have your trusty laptop with your development system and an emulator. You figure out that there was a problem with the system specifications and a symmetric FIR filter in the software won’t do the job; it needs reduced passband ripple or, maybe, more stopband attenuation. You then realize you don’t have any filter design software on the laptop, and the customer is getting angry. The answer is easy: you can take the existing filter and sharpen it. Simply stated, filter sharpening is a technique for creating a new filter from an old one [1]–[3]. While the technique is almost 30 years old, it is not generally known by DSP engineers nor is it mentioned in most DSP textbooks.

1.1 IMPROVING A DIGITAL FILTER

Before we look at filter sharpening, let’s consider the first solution that comes to mind, filtering the data twice with the existing filter. If the original filter’s transfer function is H(z), then the new transfer function (of the H(z) filter cascaded with itself) is H(z)². For example, let’s assume the original lowpass N-tap FIR filter, designed using the Parks-McClellan algorithm [4], has the following characteristics:

Number of coefficients: N = 17

Sample rate: F_s = 1

Passband width: f_pass = 0.2

Passband deviation: δ_pass = 0.05 (0.42 dB peak ripple)

Stopband frequency: f_stop = 0.3

Stopband deviation: δ_stop = 0.005 (−46 dB attenuation)

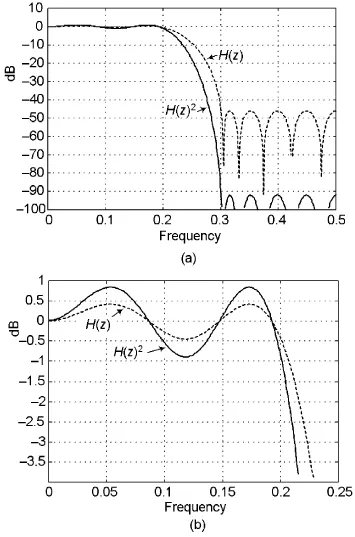
Figure 1–1(a) shows the performance of the H(z) and cascaded H(z)² filters. Everything looks okay. The new filter has the same band edges, and the stopband attenuation is increased. But what about the passband? Let’s zoom in and take a look at Figure 1–1(b). The squared filter, H(z)², has larger deviations in the passband than the original filter. In general, the squaring process will:

1. Approximately double the error (response ripple) in the passband.

2. Square the errors in the stopband (i.e., double the attenuation in dB in the stopband).

3. Leave the passband and stopband edges unchanged.

4. Approximately double the impulse response length of the original filter.

5. Maintain filter phase linearity.

Figure 1–1 H(z) and H(z)² performance: (a) full frequency response; (b) passband response.

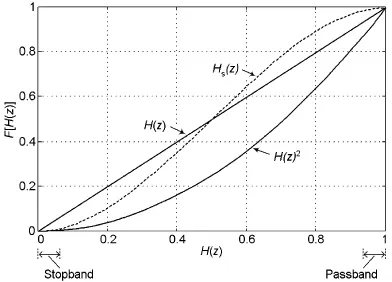
It is fairly easy to examine this operation to see the observed behavior if we view the relationship between H(z) and H(z)² in a slightly unconventional way. We can think of filter squaring as a function F[H(z)] operating on the H(z) transfer function. We can then plot the output amplitude of this function, H(z)², versus the amplitude of the input H(z) to visualize the amplitude change function.

The plot for F[H(z)] = H(z) is simple; the output is the input, so the result is the straight line as shown in Figure 1–2. The function F[H(z)] = H(z)² is a quadratic curve. When the H(z) input amplitude is near zero, the H(z)² output amplitude is closer to zero, which means the stopband attenuation is increased with H(z)². When the H(z) input amplitude is near one, the H(z)² output band is approximately twice as far away from one, which means the passband ripple is increased.

Figure 1–2 Various F[H(z)] functions operating on H(z).

The squaring process improved the stopband, but degraded the passband. The improvement was a result of the amplitude change function being horizontal at zero. So to improve H(z) in both the passband and stopband, we want the F[H(z)] amplitude function to be horizontal at both H(z) = 0 and H(z) = 1 (in other words, have a first derivative of zero at these points). This results in the output amplitude changing slower than the input amplitude as we move away from zero and one, which lowers the ripple in these areas. The simplest function that meets this will be a cubic of the form

(1–1)

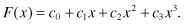
Its derivative (with respect to x) is

(1–2)

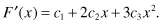
Specifying F(x) and F′(x) for the two values of x = 0 and x = 1 allows us to solve (1–1) and (1–2) for the c_n coefficients as

(1–3)

(1–4)

(1–5)

(1–6)

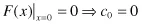
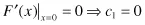
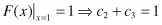
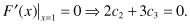
Solving (1–5) and (1–6) simultaneously yields c₂ = 3 and c₃ = –2, giving us the function

(1–7)

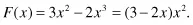
Stating this function as the sharpened filter H_s(z) in terms of H(z), we have

(1–8)

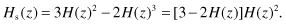
The function H_s(z) is the dotted curve in Figure 1–2.

1.2 FIR FILTER SHARPENING

H_s(z) is called the “sharpened” version of H(z). If we have a function whose z-transform is H(z), then we can outline the filter sharpening procedure, with the aid of Figure 1–3, as the following:

1. Filter the input signal, x(n), once with H(z).

2. Double the filter output sequence to obtain w(n).

3. Subtract w(n) from 3x(n) to obtain u(n).

4. Filter u(n) twice by H(z) to obtain the output y(n).

Figure 1–3 Filter sharpening p...

Table of contents

• Cover
• IEEE Press
• Title page
• Copyright page
• Dedication
• Preface
• Contributors
• Part One: Efficient Digital Filters
• Part Two: Signal and Spectrum Analysis Tricks
• Part Three: Fast Function Approximation Algorithms
• Part Four: Signal Generation Techniques
• Part Five: Assorted High-Performance DSP Techniques
• Index