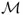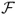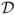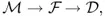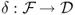Rough-Fuzzy Pattern Recognition

Applications in Bioinformatics and Medical Imaging

Pradipta Maji, Sankar K. Pal

• Publisher: Wiley-IEEE Computer Society Pr
• Year: 2011
• Print ISBN: 9781118004401
• eBook ISBN: 9781118119716
• Edition: 1
• Topic: Technology & Engineering
• Subtopic: Electrical Engineering & Telecommunications
• Index: Technology & Engineering

Learn how to apply rough-fuzzy computing techniques to solve problems in bioinformatics and medical image processing

Emphasizing applications in bioinformatics and medical image processing, this text offers a clear framework that enables readers to take advantage of the latest rough-fuzzy computing techniques to build working pattern recognition models. The authors explain step by step how to integrate rough sets with fuzzy sets in order to best manage the uncertainties in mining large data sets. Chapters are logically organized according to the major phases of pattern recognition systems development, making it easier to master such tasks as classification, clustering, and feature selection.

Rough-Fuzzy Pattern Recognition examines the important underlying theory as well as algorithms and applications, helping readers see the connections between theory and practice. The first chapter provides an introduction to pattern recognition and data mining, including the key challenges of working with high-dimensional, real-life data sets. Next, the authors explore such topics and issues as:

• Soft computing in pattern recognition and data mining
• A mathematical framework for generalized rough sets, incorporating the concept of fuzziness in defining the granules as well as the set
• Selection of non-redundant and relevant features of real-valued data sets
• Selection of the minimum set of basis strings with maximum information for amino acid sequence analysis
• Segmentation of brain MR images for visualization of human tissues

Numerous examples and case studies help readers better understand how pattern recognition models are developed and used in practice. This text—covering the latest findings as well as directions for future research—is recommended for both students and practitioners working in systems design, pattern recognition, image analysis, data mining, bioinformatics, soft computing, and computational intelligence.

Chapter 1

Introduction to Pattern Recognition and Data Mining

1.1 Introduction

Pattern recognition is an activity that human beings normally excel in. The task of pattern recognition is encountered in a wide range of human activity. In a broader perspective, the term could cover any context in which some decision or forecast is made on the basis of currently available information. Mathematically, the problem of pattern recognition deals with the construction of a procedure to be applied to a set of inputs; the procedure assigns each new input to one of a set of classes on the basis of observed features. The construction of such a procedure on an input data set is defined as pattern recognition.

A pattern typically comprises some features or essential information specific to a pattern or a class of patterns. Pattern recognition, as per the convention, is the study of how machines can observe the environment, learn to distinguish patterns of interest from their background, and make sound and reasonable decisions about the categories of the patterns. In other words, the discipline of pattern recognition essentially deals with the problem of developing algorithms and methodologies that can enable the computer implementation of many recognition tasks that humans normally perform. The objective is to perform these tasks more accurately, faster, and perhaps more economically than humans and, in many cases, to release them from drudgery resulting from performing routine recognition tasks repetitively and mechanically. The scope of pattern recognition also encompasses tasks at which humans are not good, such as reading bar codes. Hence, the goal of pattern recognition research is to devise ways and means of automating certain decision-making processes that lead to classification and recognition.

Pattern recognition can be viewed as a twofold task, consisting of learning the invariant and common properties of a set of samples characterizing a class, and of deciding that a new sample is a possible member of the class by noting that it has properties common to those of the set of samples. The task of pattern recognition can be described as a transformation from the measurement space

to the feature space

and finally to the decision space

; that is,

1.1

where the mapping

is the decision function, and the elements

are termed as decisions.

Pattern recognition has been a thriving field of research for the past few decades [1–8]. The seminal article by Kanal [9] gives a comprehensive review of the advances made in the field until the early 1970s. More recently, a review article by Jain et al. [10] provides an engrossing survey of the advances made in statistical pattern recognition till the end of the twentieth century. Although the subject has attained a very mature level during the past four decades or so, it remains green to the researchers because of continuous cross-fertilization of ideas from disciplines such as computer science, physics, neurobiology, psychology, engineering, statistics, mathematics, and cognitive science. Depending on the practical need and demand, various modern methodologies have come into being, which often supplement the classical techniques [11].

In recent years, the rapid advances made in computer technology have ensured that large sections of the world population have been able to gain easy access to computers on account of the falling costs worldwide, and their use is now commonplace in all walks of life. Government agencies and scientific, business, and commercial organizations routinely use computers, not only for computational purposes but also for storage, in massive databases, of the immense volumes of data that they routinely generate or require from other sources. Large-scale computer networking has ensured that such data has become accessible to more and more people. In other words, we are in the midst of an information explosion, and there is an urgent need for methodologies that will help us to bring some semblance of order into the phenomenal volumes of data that can readily be accessed by us with a few clicks of the keys of our computer keyboard. Traditional statistical data summarization and database management techniques are just not adequate for handling data on this scale and for intelligently extracting information, or rather, knowledge that may be useful for exploring the domain in question or the phenomena responsible for the data, and providing support to decision-making processes. This quest has thrown up a new phrase, called data mining [12–14].

The massive databases are generally characterized by the numeric as well as textual, symbolic, pictorial, and aural data. They may contain redundancy, errors, imprecision, and so on. Data mining is aimed at discovering natural structures within such massive and often heterogeneous data. It is visualized as being capable of knowledge discovery using generalizations and magnifications of existing and new pattern recognition algorithms. Therefore, pattern recognition plays a significant role in the data mining process. Data mining deals with the process of identifying valid, novel, potentially useful, and ultimately understandable patterns in data. Hence, it can be viewed as applying pattern recognition and machine learning principles in the context of voluminous, possibly heterogeneous data sets [11].

One of the important problems in real-life data analysis is uncertainty management. Some of the sources of this uncertainty include incompleteness and vagueness in class definitions. In this background, the possibility concept introduced by the fuzzy sets theory [15] and rough sets theory [16] have gained popularity in modeling and propagating uncertainty. Both the fuzzy sets and rough sets provide a mathematical framework to capture uncertainties associated with the data [17]. They are complementary in some aspects. The generalized theories of rough-fuzzy sets and fuzzy-rough sets have been applied successfully to feature selection of real-valued data [18, 19], classification [20], image processing [21], data mining [22], information retrieval [23], fuzzy decision rule extraction, and rough-fuzzy clustering [24, 25].

The objective of this book is to provide some results of investigations, both theoretical and experimental, addressing the relevance of rough-fuzzy approaches to pattern recognition with real-life applications. Various methodologies are presented, integrating fuzzy logic and rough sets for clustering, classification, and feature selection. The emphasis of these methodologies is given on (i) handling data sets which are large, both in size and dimension, and involve classes that are overlapping, intractable and/or having nonlinear boundaries; (ii) demonstrating the significance of rough-fuzzy granular computing in soft computing paradigm for dealing with the knowledge discovery aspect; and (iii) demonstrating their success in certain tasks of bioinformatics and medical imaging as an example. Before describing the scope of the book, a brief review of pattern recognition, data mining, and application of pattern recognition algorithms in data mining problems is provided.

The structure of the rest of this chapter is as follows: Section 1.2 briefly presents a description of the basic concept, features, and techniques of pattern recognition. In Section 1.3, the data mining aspect is elaborated, discussing its components, tasks involved, approaches, and application areas. The pattern recognition perspective of data mining is introduced next and related research challenges are mentioned. The role of soft computing in pattern recognition and data mining is described in Section 1.4. Finally, Section 1.5 discusses the scope and organization of the book.

1.2 Pattern Recognition

A typical pattern recognition system consists of three phases, namely, data acquisition, feature selection or extraction, and classification or clustering. In the data acquisition phase, depending on the environment within which the objects are to be classified or clustered, data are gathered using a set of sensors. These are then passed on to the feature selection or extraction phase, where the dimensionality of the data is reduced by retaining or measuring only some characteristic features or properties. In a broader perspective, this stage significantly influences the entire recognition process. Finally, in the classification or clustering phase, the selected or extracted features are passed on to the classification or clustering system that evaluates the incoming information and makes a final decision. This phase basically establishes a transformation between the features and the classes or clusters [1, 2, 8].

1.2.1 Data Acquisition

In data acquisition phase, data are gathered via a set of sensors depending on the environment within which the objects are to be classified. Pattern recognition techniques are applicable in a wide domain, where the data may be qualitative, quantitative, or both; they may be numerical, linguistic, pictorial, or any combination thereof. Generally, the data structures that are used in pattern recognition systems are of two types: object data vectors and relational data. Object data, sets of numerical vectors of m features, are represented as X = {x1, … , xi, … , xn}, a set of n feature vectors in the m-dimensional measurement space ℜm. The ith object observed in the process has vector xi as its numerical representation; xij is the jth (j = 1, … , m) feature associated with the ith object. On the other hand, relational data are a set of n2 numerical relationships, say rij, between pairs of objects. In other words, rij represents the extent to which objects xi and xj are related in the sense of some binary relationship ρ. If the objects that are pairwise related by ρ are called O = {o1, … , oi, … , on}, then ρ:O × O → ℜ.

1.2.2 Feature Selection

Feature selection or extraction is a process of selecting a map by which a sample in an m-dimensional measurement space is transformed into a point in a d-dimensional feature space, where d < m [1, 8]. Mathematically, it finds a mapping of the form y = f(x), by which a sample x = [x1, … , xj, … , xm] in an m-dimensional measurement space

is transformed into an object y = [y1, … , yj, … , yd] in a d-dimensional feature space

.

The main objective of this task is to retain or generate the optimum salient characteristics necessary for the recognition process and to reduce the dimensionality of the measurement space so that effective and easily computable algorithms can be devised for efficient classification. The problem of feature selection or extraction has two aspects, namely, formulating a suitable criterion to evaluate the goodness of a feature set and searching the optimal set in terms of the criterion. In general, those features are considered to have optimal saliencies for which interclass (respectively, intraclass) distances are maximized (respectively, minimized). The criterion for a good feature is that it should be unchanging with any other possible variation within a class, while emphasizing differences that are important in discriminating between patterns of different types.

The major mathematical measures so far devised for the estimation of feature quality are mostly statistical in nature, and can be broadly classified into two categories, namely, feature selection in the measurement space and feature selection in a transformed space. The techniques in the first category generally reduce the dimensionality of the measurement space by discarding redundant or least information-carrying features. On the other hand, those in the second category utilize all the information contained in the measurement space to obtain a new transformed space, thereby mapping a higher dimensional pattern to a lower dimensional one. This is referred to as feature extraction [1, 2, 8].

1.2.3 Classification and Clustering

The problem of classifi...

Table of contents

• Cover
• Series Page
• Title Page
• Copyright
• Dedication Page
• Foreword
• Preface
• About the Authors
• Chapter 1: Introduction to Pattern Recognition and Data Mining
• Chapter 2: Rough-Fuzzy Hybridization and Granular Computing
• Chapter 3: Rough-Fuzzy Clustering: Generalized c-Means Algorithm
• Chapter 4: Rough-Fuzzy Granulation and Pattern Classification
• Chapter 5: Fuzzy-Rough Feature Selection using f-Information Measures
• Chapter 6: Rough Fuzzy c-Medoids and Amino Acid Sequence Analysis
• Chapter 7: Clustering Functionally Similar Genes from Microarray Data
• Chapter 8: Selection of Discriminative Genes from Microarray Data
• Chapter 9: Segmentation of Brain Magnetic Resonance Images
• Index