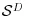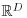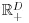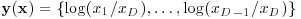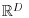Compositional Data Analysis

Theory and Applications

Vera Pawlowsky-Glahn, Antonella Buccianti, Vera Pawlowsky-Glahn, Antonella Buccianti

• Publisher: Wiley
• Year: 2011
• Print ISBN: 9780470711354
• eBook ISBN: 9781119977612
• Edition: 1
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

It is difficult to imagine that the statistical analysis of compositional data has been a major issue of concern for more than 100 years. It is even more difficult to realize that so many statisticians and users of statistics are unaware of the particular problems affecting compositional data, as well as their solutions. The issue of ``spurious correlation'', as the situation was phrased by Karl Pearson back in 1897, affects all data that measures parts of some whole, such as percentages, proportions, ppm and ppb. Such measurements are present in all fields of science, ranging from geology, biology, environmental sciences, forensic sciences, medicine and hydrology.

This book presents the history and development of compositional data analysis along with Aitchison's log-ratio approach. Compositional Data Analysis describes the state of the art both in theoretical fields as well as applications in the different fields of science.

Key Features:

• Reflects the state-of-the-art in compositional data analysis.
• Gives an overview of the historical development of compositional data analysis, as well as basic concepts and procedures.
• Looks at advances in algebra and calculus on the simplex.
• Presents applications in different fields of science, including, genomics, ecology, biology, geochemistry, planetology, chemistry and economics.
• Explores connections to correspondence analysis and the Dirichlet distribution.
• Presents a summary of three available software packages for compositional data analysis.
• Supported by an accompanying website featuring R code.

Applied scientists working on compositional data analysis in any field of science, both in academia and professionals will benefit from this book, along with graduate students in any field of science working with compositional data.

Part I

INTRODUCTION

1

A short history of compositional data analysis

John Bacon-Shone

Social Sciences Research Centre, The University of Hong Kong, Hong Kong

1.1 Introduction

Compositional data are data where the elements of the composition are non-negative and sum to unity. While the data can be generated directly (e.g. probabilities), they often arise from non-negative data (such as counts, area, volume, weights, expenditures) that have been scaled by the total of the components. Geometrically, compositional data with D components has a sample space of the regular unit D-simplex,

. The key question is whether standard multivariate analysis, which assumes that the sample space is

, is appropriate for data from this restricted sample space and if not, what is the appropriate analysis? Ironically, most multivariate data are non-negative and hence already have a sample space with a restriction to

. This chapter tries to summarize more than a century of progress towards answering this question and draws heavily on the review paper by Aitchison and Egozcue (2005).

1.2 Spurious correlation

The starting point for compositional data analysis is arguably the paper of Pearson (1897), which first identified the problem of ‘spurious correlation’ between ratios of variables. It is easy to show that if X, Y and Z are uncorrelated, then X/Z and Y/Z will not be uncorrelated. Pearson then looked at how to adjust the correlations to take into account the ‘spurious correlation’ caused by the scaling. However, this ignores the implicit constraint that scaling only makes sense if the scaling variable is either strictly positive or strictly negative. In short, this approach ignores the range of the data and does not assist in understanding the process by which the data are generated. Tanner (1949) made the essential point that a log transform of the data may avoid the problem and that checking whether the original or log transformed data follow a Normal distribution may provide some guidance as to whether a transform is needed.

Chayes (1960) later made the explicit connection between Pearson’s work and compositional data and showed that some of the correlations between components of the composition must be negative because of the unit sum constraint. However, he was unable to propose a means to model such data in a way that removed the effect of the constraint.

1.3 Log and log-ratio transforms

The first step towards modern compositional data analysis was arguably the use by McAlister (1879) of Log-Normal distributions to model data that are constrained to lie in positive real space. Interestingly, he proposed this as the law of the geometric mean (versus the Normal distribution as the law of the arithmetic mean) and pointed out the lack of practical value for variance of a variable that must be positive, which can be seen in retrospect as recognition of the need for a different metric for data from restricted sample spaces, that takes constraints into account. Instead, he emphasized the meaning of the cumulative distribution. This is by no means the only way to model data on the positive real line and competes with, for example, the Gamma and Weibull distributions. It is equivalent to taking a log transform of the data, so that the non-negative constraint is removed, and then assuming a Normal distribution. One of the key texts for the Log-Normal distribution is the book by Aitchison and Brown (1969). However, this only addresses the non-negative constraint of compositional data and does not address the unit sum constraint.

The simplest meaningful example of a composition is with just two components, so the unit-sum constraint implies that the second component is just one minus the first component. This is just the situation that arises with probabilities for a binary outcome. Cox and Snell (1989) use the logit or logistic transformation of the probability in this case, which enables the use of regression models for the logit transformed probabilities. However, it appears that nobody saw the potential for a similar approach for the more general case of compositional data until the first known reference to using the log-ratio transform to solve the constraint problem for compositional (or simplicial) data by Obenchain in a personal communication to Johnson and Kotz (Kotz et al. 2000). Indeed, Obenchain contributed to the discussion of the Royal Statistical Society paper by Aitchison (1982), where he stated that he became discouraged by the problem of zero components and thus never attempted to publish his simplex work, even though he had derived many properties of the logistic-normal distribution.

The first public introduction of the properties of the logistic-normal distribution can be found in Aitchison and Shen (1980). This distribution is written in terms of log-ratios relative to the last component, so that

follows a Multivariate Normal distribution.

Up to that time, the only known tractable distribution on the simplex was the Dirichlet distribution. However, the Dirichlet distribution has some very restrictive properties, such as complete subcompositional independence, i.e. for each possible partition of the composition, the set of all its subcompositions must be independent. This makes it impossible to model any reasonable dependence structure for compositional data using the Dirichlet distribution. In contrast, the logistic-normal distribution yields a distribution on the interior of the simplex that does not require these inflexible properties, but instead they become testable linear hypotheses on the covariance matrix within a broad flexible modelling framework. In addition, the Aitchison and Shen (1980) paper showed that the logistic-normal distribution is close to any Dirichlet distribution in terms of the Kullback–Leibler divergence. Later Aitchison (1985) derived a more general distribution that contains both the Dirichlet and logistic-normal distributions, although the potential for using this distribution for testing Dirichlet against logistic-normal distributions within the same class is diminished as these hypotheses are on the boundary of the parameter space. More recently, the generalization of the logistic-normal distribution to the additive logistic skew-normal distribution on the simplex (Mateu-Figueras et al. 2005) applies the skew-normal distribution (Azzalini 2005) to log-ratios on the simplex and offers the useful possibility of modelling data where the distribution of y(x) is not symmetrical. Use of the logistic-normal distribution opens up the full range of linear modelling available for the multivariate Normal distribution in

.

1.4 Subcompositional dependence

As mentioned above, the ...

Table of contents

• Cover
• Title Page
• Copyright
• Dedication
• Preface
• List of contributors
• Part I: INTRODUCTION
• Part II: THEORY – STATISTICAL MODELLING
• Part III: THEORY – ALGEBRA AND CALCULUS
• Part IV: APPLICATIONS
• Part V: SOFTWARE
• Index