Modelling Under Risk and Uncertainty

An Introduction to Statistical, Phenomenological and Computational Methods

Etienne de Rocquigny

• Publisher: Wiley
• Year: 2012
• Print ISBN: 9780470695142
• eBook ISBN: 9781119941651
• Edition: 1
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

Modelling has permeated virtually all areas of industrial, environmental, economic, bio-medical or civil engineering: yet the use of models for decision-making raises a number of issues to which this book is dedicated:

How uncertain is my model? Is it truly valuable to support decision-making? What kind of decision can be truly supported and how can I handle residual uncertainty? How much refined should the mathematical description be, given the true data limitations? Could the uncertainty be reduced through more data, increased modeling investment or computational budget? Should it be reduced now or later? How robust is the analysis or the computational methods involved? Should / could those methods be more robust? Does it make sense to handle uncertainty, risk, lack of knowledge, variability or errors altogether? How reasonable is the choice of probabilistic modeling for rare events? How rare are the events to be considered? How far does it make sense to handle extreme events and elaborate confidence figures? Can I take advantage of expert / phenomenological knowledge to tighten the probabilistic figures? Are there connex domains that could provide models or inspiration for my problem?

Written by a leader at the crossroads of industry, academia and engineering, and based on decades of multi-disciplinary field experience, Modelling Under Risk and Uncertainty gives a self-consistent introduction to the methods involved by any type of modeling development acknowledging the inevitable uncertainty and associated risks. It goes beyond the "black-box" view that some analysts, modelers, risk experts or statisticians develop on the underlying phenomenology of the environmental or industrial processes, without valuing enough their physical properties and inner modelling potential nor challenging the practical plausibility of mathematical hypotheses; conversely it is also to attract environmental or engineering modellers to better handle model confidence issues through finer statistical and risk analysis material taking advantage of advanced scientific computing, to face new regulations departing from deterministic design or support robust decision-making.

Modelling Under Risk and Uncertainty:

• Addresses a concern of growing interest for large industries, environmentalists or analysts: robust modeling for decision-making in complex systems.
• Gives new insights into the peculiar mathematical and computational challenges generated by recent industrial safety or environmental control analysis for rare events.
• Implements decision theory choices differentiating or aggregating the dimensions of risk/aleatory and epistemic uncertainty through a consistent multi-disciplinary set of statistical estimation, physical modelling, robust computation and risk analysis.
• Provides an original review of the advanced inverse probabilistic approaches for model identification, calibration or data assimilation, key to digest fast-growing multi-physical data acquisition.
• Illustrated with one favourite pedagogical example crossing natural risk, engineering and economics, developed throughout the book to facilitate the reading and understanding.
• Supports Master/PhD-level course as well as advanced tutorials for professional training

Analysts and researchers in numerical modeling, applied statistics, scientific computing, reliability, advanced engineering, natural risk or environmental science will benefit from this book.

Chapter 1

Applications and Practices of Modelling, Risk and Uncertainty

This chapter reviews classical practice in various domains involving modelling in the context of risk and uncertainty and illustrates its common and distinguishing features. In particular, the distinct model formulations, probabilistic settings and decisional treatments encountered are reviewed in association with the typical regulatory requirements in the areas of natural risk, industrial design, reliability, risk analysis, metrology, environmental emissions and economic forecasting. This will help to introduce the notation and concepts that will be assembled within the generic modelling framework developed in Chapter 2. It will also lead to a review of the associated challenges discussed in other chapters. Although unnecessary to an understanding of the rest of the book, Chapter 1 can thus be read as an overview of the areas motivating the book's applications and as an analysis of the corresponding state of the art.

In order to facilitate reading, the following sections group the review of methods and practices under subsections that refer to given classes. Obviously, some of the methods introduced in association with one field are in fact used elsewhere, but this would not be the dominant practice. Industrial risk denotes risks affecting industrial facilities as the consequence of internal initiators such as reservoir failure, pipe break and so on; on the other hand, natural risk covers risks triggered by natural aggressions (e.g. seism, flood, . . .) and impacting on either industrial facilities or domestic installations. At the crossroads lies the so-called natech risk amongst which the Fukushima/Sendai event is a recent example.

1.1 Protection Against Natural Risk

Natural risk, an important concern for industrial or domestic facilities, has triggered an extensive field of risk research for which the ultimate goal is generally the design of protection for infrastructures or the reduction of the level of vulnerability in existing installations. Probabilistic approaches have permeated to a various extent both regulation and engineering practice, for example with regard to nuclear or hydro power facilities. Here are some notable examples of natural risk addressed:

• flood protection,
• maritime aggressions, such as waves or storm surges coupled with extreme tides,
• extreme winds,
• low flows or high temperatures (threatening the cooling of energy facilities),
• extremely cold temperatures, or associated phenomena (ice blocking, . . .),
• seism.

The typical situation is depicted in Figure 1.1. The box called ‘local risk situation’ summarises all phenomena according to which a flood, seism, cold wave or any type of aggression may impact locally on the installation and generate undesired consequences. It is determined both by:

• the natural hazard events (flood, seism, wind series . . .) that constitute initiators of the risk phenomenon;
• the local configuration of the installation, that is its vulnerability depending on the local mechanics of the natural event and its consequences depending on the assets of all kinds that are at stake (plant operation, integrity of equipments, resulting pollution or damage to the environment, potential injuries or fatalities, . . .) and the level of protection insured by the design choices and protection variables (e.g. dike height).

Natural initiators can be generally described by a few variables such as wind speed, seismic acceleration, flood flow and so on: they will be subsequently gathered inside a vector¹ xⁱⁿ. Similarly, all protection/design variables will be formally gathered inside a vector d. Additionally, official regulations or design guidelines generally specify risk or design criteria that drive the whole study process. The definition of such criteria combines the following elements:

• A given undesirable event of interest (e.i.) which will be denoted as E. Think of dike overflow caused by flood or marine surge, structural collapse, cooling system failure and so on. Such an event of interest is technically defined on the basis of critical thresholds for one or several variables of interest (v.i.) characterizing the local risk situation: they are represented in Figure 1.1 by vector z. Think of the flood water level, a margin to mechanical failure, a critical local temperature and so on.
• A maximal acceptable level of risk: for instance, the undesired event should not occur up to the 1000-yr flood, or for the seism of reference; or else, structural collapse should occur less than 10^−x per year of operation and so on.

The type of structure shown in Figure 1.1, linking variables and risk criteria, is similar to that mentioned in the book's introduction. Beyond natural risk, it will be repeated with limited variations throughout the areas reviewed in this chapter and will receive a detailed mathematical definition in Chapter 2.

Figure 1.1 Protection against natural risk – schematisation.

1.1.1 The Popular ‘Initiator/Frequency Approach’

A considerable literature has developed on the issues raised by protection against natural risk: this includes advanced probabilistic models, decision theory approaches or even socio-political considerations about the quantification of acceptable risk levels (e.g. Yen and Tung, 1993; Duckstein and Parent, 1994; Apel et al., 2004; Pappenberger and Beven, 2006). The most recent discussions have focused on the cases of major vulnerability, uncertainty about the phenomena, reversibility or the precautionary principle (Dupuy, 2002). Notwithstanding all these research developments, it is useful to start with the state of the practice in regulatory and engineering matters. Most of the time, emphasis appears to be given to a form of ‘initiator/frequency approach’ which consists of attaching the definition of the risk criterion to a reference level prescribed for the initiator, for instance:

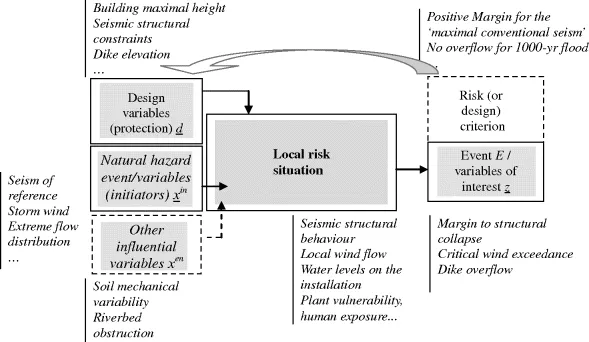
• ‘overspill should not occur for the 1000-yr flood’,
• ‘mechanical failure margin should remain positive for the reference seism’.

As will be made clear later, this consists essentially of choosing to focus on a single initiator xⁱⁿ as the dominant alea or source of randomness controlling the hazards and the risk situation. Good examples are the extreme wind speed, the flood flow, the external seismic scenario and so on. Nevertheless, a closer look into the realisation of the undesired event E usually leads to identifying other potentially important sources of uncertainties or risk factors. Yet, those additional uncertain variables (which will be noted x^en) may be separated and given an ancillary role if they are mentioned at all. Think of:

• the riverbed elevation which conditions the amount of overspill for a given level of flood flow;
• the soil conditions around the industrial facility that modify the seismic response;
• the vulnerability of the installations, or conversely the conditional efficiency of protection measures.

At most, the two former types of variability would be studied in the context of local sensitivity to the design, if not ignored or packed within an additional informal margin (e.g. add 20 cm to design water level, add 20 % to seismic loading, etc.). The latter type is seldom mentioned and is even less often included in the regulatory framework.

This has a strong impact on the probabilistic formulation of the approach. Consider the undesired event E characterised by the variables of interest z (e.g. flood level, peak temperature, peak wind velocity, mechanical margin to failure). Event E is often schematised as a mathematical set stating that a certain threshold (e.g. dike level, critical temperature, critical wind, zero margin) is exceed...

Table of contents

• Cover
• Wiley Series in Probability and Statistics
• Title Page
• Copyright
• Dedication
• Preface
• Acknowledgements
• Introduction and Reading Guide
• Notation
• Acronyms and Abbreviations
• Chapter 1: Applications and Practices of Modelling, Risk and Uncertainty
• Chapter 2: A Generic Modelling Framework
• Chapter 3: A Generic Tutorial Example: Natural Risk in an Industrial Installation
• Chapter 4: Understanding Natures of Uncertainty, Risk Margins and Time Bases for Probabilistic Decision-Making
• Chapter 5: Direct Statistical Estimation Techniques
• Chapter 6: Combined Model Estimation Through Inverse Techniques
• Chapter 7: Computational Methods for Risk and Uncertainty Propagation
• Chapter 8: Optimising under Uncertainty: Economics and Computational Challenges
• Chapter 9: Conclusion: Perspectives of Modelling in the Context of Risk and Uncertainty and Further Research
• Chapter 10: Annexes
• Epilogue
• Index
• WILEY SERIES IN PROBABILITY AND STATISTICS