Qualitative Spatial and Temporal Reasoning

Gérard Ligozat

• Publisher: Wiley-ISTE
• Year: 2013
• Print ISBN: 9781848212527
• eBook ISBN: 9781118601563
• Edition: 1
• Topic: Computer Science
• Subtopic: Computer Science General
• Index: Computer Science

Starting with an updated description of Allen's calculus, the book proceeds with a description of the main qualitative calculi which have been developed over the last two decades.  It describes the connection of complexity issues to geometric properties. Models of the formalisms are described using the algebraic notion of weak representations of the associated algebras. The book also includes a presentation of fuzzy extensions of qualitative calculi, and a description of the study of complexity in terms of clones of operations.

Chapter 1

Allen's Calculus

1.1. Introduction

The story of qualitative temporal and spatial reasoning begins with the publication of Allen's 1983 paper [ALL 83]. In this chapter and the following one, we give an introduction to Allen's calculus, and take stock of the current state of knowledge on the subject. The past 25 years have witnessed a steady development of results and techniques for reasoning about time and space in a qualitative way. For a view of the state of knowledge on this subject by the late 1980s, the reader can refer to [BBS 89b].

1.1.1. “The mystery of the dark room”

In [ALL 83], Allen introduces his calculus by using the following anecdote:

1) John was not in the room when I touched the switch to turn on the light;

2) But John was in the room later while the light went out.

1.1.1.1. Representation

These two sentences refer to three events, which in turn correspond to three time intervals: Let S (for “switch”) be a short time interval during which the switch was pressed, an interval L (for “light”) corresponding to the period when the light was on, and an interval R (for “room”) during which John was present in the room. Moreover, the two sentences provide qualitative (qualitative, i.e. not involving measurements) information about the relationships between the three time intervals I, L, and J.

What indeed can we deduce from these sentences?

Figure 1.1. When I pressed the switch …

According to sentence 1, there is no overlapping of the time intervals S and R. Moreover, our common sense informs us that the light was on in the room at a time soon after I started to press the switch and also not later than the time when I released the pressure on the switch.

If we consider all possible relations between two intervals based only on the relative orderings of their starting and ending points, we get the 13 relations represented in Figure 1.2. These 13 relations are called Allen's basic relations.

Figure 1.2. Allen's 13 basic relations between interval x (in gray) and interval y (in white)

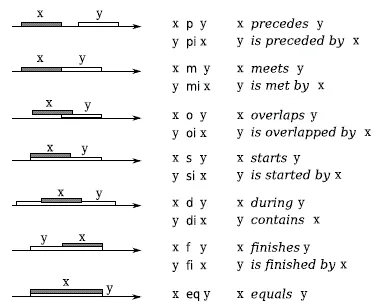
The information obtained from sentence 1 of Allen's example is not sufficiently precise to be expressed in terms of Allen's basic relations, but only in terms of disjunctions between these relations. These disjunctions are noted as subsets of the basic relations. For example, from sentence 1, we can deduce that the relationship between S and R corresponds to the set {p, m, pi, mi} (expressing the fact that I and J are disjoint), and that the relationship between S and L corresponds to the set {o, m}.

In a similar manner, from sentence 2, we can deduce that the relationship between L and R corresponds to the set {o, s, d}.

More precisely, we will express our knowledge about the existing relations in terms of constraint networks. In our case, we will consider a network with three nodes representing the time intervals S, L, and R, and arcs labeled by subsets of Allen's basic relations to express the constraints between these intervals. Hence we get the following labels:

– on the arc (S, R), the constraint {p, m, pi, mi};

– on the arc (S, L), the constraint {m, o};

– on the arc (L, R), the constraint {o, s, d}.

Figure 1.3 (a) represents the network thus obtained.

Figure 1.3. The dark room: initial constraints between the three intervals S, L, and R (a); constraint on the arc (L, R) by composition (b); after intersection, the constraint on (L, R) is {o, s}; by composition, {p, m, o} on (S, R) is obtained (c); after intersection with the initial constraint on (S, R) (d)

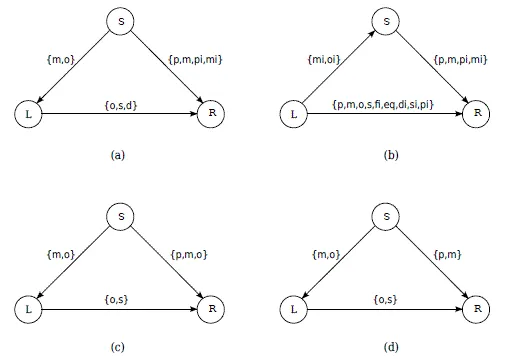
1.1.1.2. Reasoning: constraint propagation

In a manner similar to what we discussed for the time point calculus in the Introduction, two natural operations are possible for Allen's relations: the inversion operation and the composition operation. For example, by inverting the constraint {m, o} on the arc (S, L), tlie constraint {mi, oi} on the arc (L, S) can be deduced. We now have a set of possible basic relations between L and S, and another set of possible basic relationships between S and R. The operation of composition will allow us to infer a set of possible relations between L and R from this knowledge. The results of the composition of two basic relations can be tabulated, resulting in a table called the composition table of Allen's calculus (originally called table of transitivity by Allen). Using the composition table, we get the constraint {p, m, o, s, fi, eq, di, si, pi} on the arc...

Table of contents

• Cover
• Title Page
• Copyright
• Introduction: Qualitative Reasoning
• Chapter 1: Allen‘s Calculus
• Chapter 2: Polynomial Subclasses of Allen‘s Algebra
• Chapter 3: Generalized Intervals
• Chapter 4: Binary Qualitative Formalisms
• Chapter 5: Qualitative Formalisms of Arity Greater than 2
• Chapter 6: Quantitative Formalisms, Hybrids, and Granularity
• Chapter 7: Fuzzy Reasoning
• Chapter 8: The Geometrical Approach and Conceptual Spaces
• Chapter 9: Weak Representations
• Chapter 10: Models of RCC-8
• Chapter 11: A Categorical Approach of Qualitative Reasoning
• Chapter 12: Complexity of Constraint Languages
• Chapter 13: Spatial Reasoning and Modal Logic
• Chapter 14: Applications and Software Tools
• Chapter 15: Conclusion and Prospects
• Appendix A: Elements of Topology
• Appendix B: Elements of Universal Algebra
• Appendix C: Disjunctive Linear Relations
• Bibliography
• Index