Introduction to Stochastic Analysis

Integrals and Differential Equations

Vigirdas Mackevicius

• Publisher: Wiley-ISTE
• Year: 2013
• Print ISBN:
  9781848213111
• Edition: 1
• eBook ISBN:
  9781118603246
• Topic: Mathematics
• Subtopic: Functional Analysis
• Index: Mathematics

This is an introduction to stochastic integration and stochastic differential equations written in an understandable way for a wide audience, from students of mathematics to practitioners in biology, chemistry, physics, and finances. The presentation is based on the naïve stochastic integration, rather than on abstract theories of measure and stochastic processes. The proofs are rather simple for practitioners and, at the same time, rather rigorous for mathematicians. Detailed application examples in natural sciences and finance are presented. Much attention is paid to simulation diffusion processes.
The topics covered include Brownian motion; motivation of stochastic models with Brownian motion; Itô and Stratonovich stochastic integrals, Itô's formula; stochastic differential equations (SDEs); solutions of SDEs as Markov processes; application examples in physical sciences and finance; simulation of solutions of SDEs (strong and weak approximations). Exercises with hints and/or solutions are also provided.

Chapter 1

Introduction: Basic Notions of Probability Theory

1.1. Probability space

The main notion of probability theory is a probability space (Ω,

, P) consisting of any set of elementary events (or outcomes) Ω, a system of events

, and probability measure P. Though these objects form an unanimous whole, we shall try to consider them separately.

Sample space Ω is any non-empty set. Its elements are interpreted as all possible outcomes of an experiment (test, monitoring, phenomenon, and so on) and are called outcomes or elementary events. They are often denoted by letter ω (possibly with some index(es)). Let us consider some examples.

EXAMPLE 1A. Suppose that our experiment involves throwing a die once. Usually, we are only interested in the number of dots, and so all possible outcomes can be described by the sample space Ω = {1, 2, 3, 4, 5, 6}. Naturally, the outcome of the experiment “the number of dots that appeared on top is five” is represented by the simple event ω = 5.

EXAMPLE 1B. Consider the more complex experiment of throwing a die thrice. It can be described by the sample space consisting of all triples (i , j, k) of the natural numbers from 1 to 6 (the number of such triples is 6³ = 216):

EXAMPLE 1C. If a die is thrown an unknown (in advance) number of times (for example, until six dots appear three consecutive times or until we are tired of throwing), it is convenient to consider the abstract model with unlimited number of dice throws. An outcome of such an “experiment” can be described by a sequence ω= {ω_n} = {ω₁,ω₂,..}, the elements ω_n of which are arbitrary natural numbers from 1 to 6. Thus, in this case, the sample space is the set of all such sequences:

EXAMPLE 2A. Suppose that we decided to measure the outdoor temperature. An outcome of the “experiment” could be the temperature at a fixed moment in time. Since, practically, the temperature cannot be lower than (say) −60°C and higher than +60°C, for this experiment, we can consider the sample space Ω = [− 60, 60]. However, it is often more convenient not to define any reasonable bounds for the temperature (perhaps we measure the temperature in Mars or in the center of the Sun) and take Ω =

.

EXAMPLE 2B. Let us measure the outdoor temperature each hour for the whole day. Then the outcome of the experiment is a set of 24 numbers meaning the temperatures at time moments t = 1, 2,… , 24, and a...

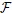
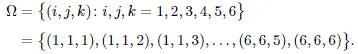
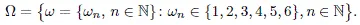
Table of contents

• Cover
• Title Page
• Copyright
• Preface
• Notation
• Chapter 1: Introduction: Basic Notions of Probability Theory
• Chapter 2: Brownian Motion
• Chapter 3: Stochastic Models with Brownian Motion and White Noise
• Chapter 4: Stochastic Integral with Respect to Brownian Motion
• Chapter 5: Itô's Formula
• Chapter 6: Stochastic Differential Equations
• Chapter 7: Itô Processes
• Chapter 8: Stratonovich Integral and Equations
• Chapter 9: Linear Stochastic Differential Equations
• Chapter 10: Solutions of SDEs as Markov Diffusion Processes
• Chapter 11: Examples
• Chapter 12: Example in Finance: Black–Scholes Model
• Chapter 13: Numerical Solution of Stochastic Differential Equations
• Chapter 14: Elements of Multidimensional Stochastic Analysis
• Solutions, Hints, and Answers
• Bibliography
• Index