Fundamentals of Stochastic Networks

Oliver C. Ibe

• Publisher: Wiley
• Year: 2011
• Print ISBN: 9781118065679
• eBook ISBN: 9781118092989
• Edition: 1
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

An interdisciplinary approach to understanding queueing and graphical networks

In today's era of interdisciplinary studies and research activities, network models are becoming increasingly important in various areas where they have not regularly been used. Combining techniques from stochastic processes and graph theory to analyze the behavior of networks, Fundamentals of Stochastic Networks provides an interdisciplinary approach by including practical applications of these stochastic networks in various fields of study, from engineering and operations management to communications and the physical sciences.

The author uniquely unites different types of stochastic, queueing, and graphical networks that are typically studied independently of each other. With balanced coverage, the book is organized into three succinct parts:

• Part I introduces basic concepts in probability and stochastic processes, with coverage on counting, Poisson, renewal, and Markov processes
  
  

• Part II addresses basic queueing theory, with a focus on Markovian queueing systems and also explores advanced queueing theory, queueing networks, and approximations of queueing networks
  
  

• Part III focuses on graphical models, presenting an introduction to graph theory along with Bayesian, Boolean, and random networks
  
  

The author presents the material in a self-contained style that helps readers apply the presented methods and techniques to science and engineering applications. Numerous practical examples are also provided throughout, including all related mathematical details.

Featuring basic results without heavy emphasis on proving theorems, Fundamentals of Stochastic Networks is a suitable book for courses on probability and stochastic networks, stochastic network calculus, and stochastic network optimization at the upper-undergraduate and graduate levels. The book also serves as a reference for researchers and network professionals who would like to learn more about the general principles of stochastic networks.

1

BASIC CONCEPTS IN PROBABILITY

1.1 INTRODUCTION

The concepts of experiments and events are very important in the study of probability. In probability, an experiment is any process of trial and observation. An experiment whose outcome is uncertain before it is performed is called a random experiment. When we perform a random experiment, the collection of possible elementary outcomes is called the sample space of the experiment, which is usually denoted by Ω. We define these outcomes as elementary outcomes because exactly one of the outcomes occurs when the experiment is performed. The elementary outcomes of an experiment are called the sample points of the sample space and are denoted by w_i, i = 1, 2, … If there are n possible outcomes of an experiment, then the sample space is Ω = {w₁, w₂, … , w_n}. An event is the occurrence of either a prescribed outcome or any one of a number of possible outcomes of an experiment. Thus, an event is a subset of the sample space.

1.2 RANDOM VARIABLES

Consider a random experiment with sample space Ω. Let w be a sample point in Ω. We are interested in assigning a real number to each w ∈ Ω. A random variable, X(w), is a single-valued real function that assigns a real number, called the value of X(w), to each sample point w ∈ Ω. That is, it is a mapping of the sample space onto the real line.

Generally a random variable is represented by a single letter X instead of the function X(w). Therefore, in the remainder of the book we use X to denote a random variable. The sample space Ω is called the domain of the random variable X. Also, the collection of all numbers that are values of X is called the range of the random variable X.

Let X be a random variable and x a fixed real value. Let the event A_x define the subset of Ω that consists of all real sample points to which the random variable X assigns the number x.

That is,

Since A_x is an event, it will have a probability, which we define as follows:

We can define other types of events in terms of a random variable. For fixed numbers x, a, and b, we can define the following:

These events have probabilities that are denoted by

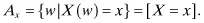
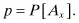
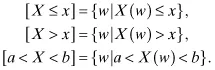
• P[X ≤ x] is the probability that X takes a value less than or equal to x.
• P[X > x] is the probability that X takes a value greater than x; this is equal to 1 – P[X ≤ x].
• P[a < X < b] is the probability that X takes a value that strictly lies between a and b.

1.2.1 Distribution Functions

Let X be a random variable and x be a number. As stated earlier, we can define the event [X ≤ x] = {x|X(w) ≤ x}. The distribution function (or the cumulative distribution function [CDF]) of X is defined by:

Tha...

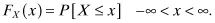
Table of contents

• Cover
• Title page
• Copyright page
• PREFACE
• 1 BASIC CONCEPTS IN PROBABILITY
• 2 OVERVIEW OF STOCHASTIC PROCESSES
• 3 ELEMENTARY QUEUEING THEORY
• 4 ADVANCED QUEUEING THEORY
• 5 QUEUEING NETWORKS
• 6 APPROXIMATIONS OF QUEUEING SYSTEMS AND NETWORKS
• 7 ELEMENTS OF GRAPH THEORY
• 8 BAYESIAN NETWORKS
• 9 BOOLEAN NETWORKS
• 10 RANDOM NETWORKS
• REFERENCES
• Index
• Download CD/DVD content