Models for Bonding in Chemistry

Valerio Magnasco, Valerio Magnasco

• Publisher: Wiley
• Year: 2011
• Print ISBN: 9780470667033, 9780470667026
• eBook ISBN: 9781119957348
• Edition: 1
• Topic: Sciences physiques
• Subtopic: Chimie physique et théorique

A readable little book assisting the student in understanding, in a nonmathematical way, the essentials of the different bonds occurring in chemistry. Starting with a short, self-contained, introduction, Chapter 1 presents the essential elements of the variation approach to either total or second-order molecular energies, the system of atomic units (au) necessary to simplify all mathematical expressions, and an introductory description of the electron distribution in molecules. Using mostly 2x2 Hückel secular equations, Chapter 2, by far the largest part of the book because of the many implications of the chemical bond, introduces a model of bonding in homonuclear and heteronuclear diatomics, multiple and delocalized bonds in hydrocarbons, and the stereochemistry of chemical bonds in polyatomic molecules, in a word, a model of the strong first-order interactions originating the chemical bond. In Chapter 3 the Hückel model of the linear polyene chain is used to explain the origin of band structure in the 1-dimensional crystal. Chapter 4 deals with a simple two-state model of weak interactions, introducing the reader to understand second-order electric properties of molecules and VdW bonding between closed shells. Lastly, Chapter 5 studies the structure of H-bonded dimers and the nature of the hydrogen bond, which has a strength intermediate between a VdW bond and a weak chemical bond. Besides a qualitative MO approach based on HOMO-LUMO charge transfer from an electron donor to an electron acceptor molecule, a quantitative electrostatic approach is presented yielding an electrostatic model working even at its simplest pictorial level. A list of alphabetically ordered references, author and subject indices complete the book.

1

Mathematical Foundations

1.1 Matrices and Systems of Linear Equations

1.2 Properties of Eigenvalues and Eigenvectors

1.3 Variational Approximations

1.4 Atomic Units

1.5 The Electron Distribution in Molecules

1.6 Exchange-overlap Densities and the Chemical Bond

In physics and chemistry it is not possible to develop any useful model of matter without a basic knowledge of some elementary mathematics. This involves use of some elements of linear algebra, such as the solution of algebraic equations (at least quadratic), the solution of systems of linear equations, and a few elements on matrices and determinants.

1.1 MATRICES AND SYSTEMS OF LINEAR EQUATIONS

We start from matrices, limiting ourselves to the case of a square matrix of order two, namely a matrix involving two rows and two columns. Let us denote this matrix by the boldface capital letter A:

(1.1)

where A_ij is a number called the ijth element of matrix A. The elements A_ii (j = i) are called diagonal elements. We are interested mostly in symmetric matrices, for which A₂₁ = A₁₂· If A₂₁ = A₁₂ = 0, the matrix is diagonal. Properties of a square matrix A are its trace(tr A = A₁₁ + A₂₂), the sum of its diagonal elements, and its determinant,denoted by |A| = det A, a number that can be evaluated from its elements by the rule:

(1.2)

Two 2 × 2 matrices can be multiplied rows by columns by the rule:

(1.3)

(1.4)

the elements of the product matrix C being:

(1.5)

So, we are led to the matrix multiplication rule:

(1.6)

If matrix B is a simple number a, Equation (1.6) shows that all elements of matrix A must be multiplied by this number. Instead, for a|A|, we have from Equation (1.2):

(1.7)

so that, multiplying a determinant by a number is equivalent to multiplying just one row (or one column) by that number.

We can have also rectangular matrices, where the number of rows is different from the number of columns. Particularly important is the 2 ×1 column vector c:

(1.8)

or the 1 × 2 row vector C:

(1.9)

where the tilde ~ means interchanging columns by rows or vice versa (the transposed matrix).

The linear inhomogeneous system:

(1.10)

can be easily rewritten in matrix form using matrix multiplication rule (1.3) as:

(1.11)

where c and b are 2 × 1 column vectors.

Equation (1.10) is a system of two algebraic equations linear in the unknowns c₁ and c₂, the elements of matrix A being the coefficients of the linear combination. Particular importance has the case where b is proportional to c through a number λ:

(1.12)

which is known as the eigenvalue equation for matrix A. λ is called an eigenvalue and c an eigenvector of the square matrix A. Equation (1.12) is equally well written as the homogeneous system:

(1.13)

where 1 is the 2 × 2 diagonal matrix having 1 along the diagonal, called the identity matrix, and 0 is the zero vector matrix, a 2 × 1 column of zeros. Written explicitly, the homogen...

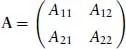
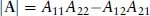
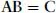
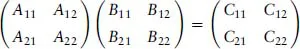
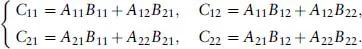
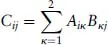
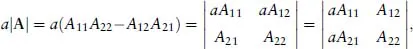
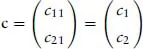
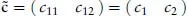
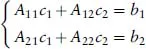
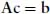
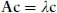
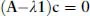
Table of contents

• Cover
• Title page
• Copyright
• Dedication
• Preface
• 1: Mathematical Foundations
• Part 1: Short-range Interactions
• Part 2: Long-Range Interactions
• References
• Author Index
• Subject Index