Colliding Plane Waves in General Relativity

J.B. Griffiths

• Publisher: Dover Publications
• Year: 2016
• ISBN:
  9780486810980
• Topic: Ciencias físicas
• Subtopic: Relatividad en física

This monograph surveys recent research on the collision and interaction of gravitational and electromagnetic waves. "This is a particularly important topic in general relativity, " the author notes, "since the theory predicts that there will be a nonlinear interaction between such waves." Geared toward graduate students and researchers in general relativity, the text offers a comprehensive and unified review of the vast literature on the subject.
The first eight chapters offer background, presenting the field equations and discussing some qualitative aspects of their solution. Subsequent chapters explore further exact solutions for colliding plane gravitational waves and the collision and interaction of electromagnetic waves. The final chapters summarize all related results for the collision of plane waves of different types and in non-flat backgrounds. A new postscript updates developments since the book's initial 1991 publication.

1

INTRODUCTION

The subject to be discussed in this book is the collision and interaction of gravitational and electromagnetic waves. This is a particularly important topic in general relativity since the theory predicts that there will be a non-linear interaction between such waves. The effect of the non-linearity however, is unclear. It is appropriate therefore to look in some detail at the simplest possible situation in which the effect of the non-linearity will be manifest: namely the interaction between colliding plane waves.

1.1 Why consider wave interactions?

In classical theory, Maxwell’s equations are linear. An immediate consequence of this is that solutions can be simply superposed. This leads to the prediction that electromagnetic waves pass through each other without any interaction. This prediction is very thoroughly confirmed by observations. Radio waves are transmitted at many different frequencies, yet it is possible for a receiver to select any one particular station and to receive that signal almost exactly as it was transmitted. The only interference that is detected arises from other transmitters using the same frequency, and from the difficulty of isolating just one frequency within the receiver.

After many years’ experience, no interaction has ever been detected between propagating electromagnetic waves. This applies not just to radio waves, but to all types of electromagnetic radiation, including light. That we can see clearly through a vacuum, even though light is also passing through it in other directions undetected, is one of the best established of scientific observations. More remarkably, this applies not just to local phenomena, but to the vast regions of space. The light that reaches us from distant galaxies arrives without any apparent interaction with the light that must have crossed its path during the millions of years that it takes to reach us. The apparent linearity of the field equations for electromagnetic waves is thus one of the best established scientific facts.

However, this is not the entire story Einstein’s equations which describe gravitational fields are highly non-linear. It follows that gravitational waves, if they exist, cannot pass through each other without a significant interaction. In this book we will be using the standard general theory of relativity. In this theory gravitational waves are predicted, though their magnitudes are so small that the possibility of detecting them is only just coming within the scope of the most sophisticated modern apparatus. The purpose of this book is to contribute to an understanding of the character of the interaction that is theoretically predicted between gravitational waves.

In Einstein’s theory, gravitational waves are considered as perturbations of space-time curvature that propagate with the speed of light. As these waves pass through each other, theoretically there will be a nonlinear interaction through the gravitational field equations. It will be necessary to consider the general character of these interactions, and how the propagating waves are modified by them.

Consider again electromagnetic waves. According to Einstein’s theory, all forms of energy have an associated gravitational field. Electromagnetic waves must therefore be coupled to an associated perturbation in the space-time curvature. In the full Einstein-Maxwell theory, Maxwell’s equations describing the electromagnetic field remain linear, indicating that there is no direct electromagnetic interaction between waves. However, Einstein’s equations, which apply to the gravitational field, are highly non-linear. Thus, as two electromagnetic waves pass through each other, there will be a non-linear interaction between them due to their associated gravitational fields.

This non-linear interaction between electromagnetic waves that is predicted by Einstein’s theory must necessarily be very small in order to be consistent with the fact that such interactions have not yet been detected. An interaction, however, is predicted, though its magnitude is likely to be similar to that between gravitational waves.

Since the interactions we will be considering are so weak, it may be considered appropriate initially to use approximation techniques. A number of authors have considered this approach. The modern techniques of numerical relativity have also produced some interesting results. However, these approaches will not be used in this book. The method adopted here will be to concentrate on exact solutions of the Einstein-Maxwell field equations. This has the advantage of being able to clarify something of the global structure of wave interactions. This turns out to be one of their most remarkable features. It leaves us, however, with the problem of finding exact solutions, and these are only possible in a very limited number of situations.

1.2 Simplifying assumptions

The problem that is to be considered in this book is the interaction between two waves. A simple case in which the waves propagate in the same direction has been analysed by Bonnor (1969) and Aichelburg (1971). They have found that, for the class of vacuum pp-waves that will be defined in Section 4.1, the waves can be simply superposed without interaction because of the linearity of the field equations when written in a certain privileged class of coordinate system.

It is therefore appropriate to concentrate on the general case in which the waves propagate in arbitrary different directions. In this case it is always possible to make a Lorentz transformation to a frame of reference in which the waves approach each other from exactly opposite spatial directions. It is therefore only necessary to consider the ‘head on’ collision between the two waves. However, even this situation is too difficult to analyse without some further simplifying assumptions.

In order to obtain exact solutions, it is appropriate initially to make the additional assumption that the approaching waves have plane symmetry. This is a very severe restriction indeed, even though we intuitively think of plane fronted waves as approximations to spherical waves at large distances from their sources. However, the two cases must be distinguished as their global features are totally different.

The waves we will be considering not only have a plane wave front, but also have infinite extent in all directions in the plane. In contrast, waves generated by finite sources must have curved wave fronts, but it is very difficult to set up boundary conditions and field equations for the interactions between such waves. The reason for concentrating on plane waves is that in this case it is possible to formulate the problem explicitly and to find exact solutions.

In addition to the assumption that the wave front is plane, the imposition of plane symmetry also requires that the magnitude of the wave is constant over the entire plane. Further, it is appropriate to concentrate on ‘head on’ collisions and thus to impose the condition of global plane symmetry. It is always possible to make a Lorentz transformation to include oblique collisions but the physical interpretation of the solutions is now severely restricted by the above assumptions.

The situation being considered in this book is thus the very restrictive one in which two waves, each with plane symmetry, approach each other from exactly opposite directions. A topic of further research will be to consider how to apply the qualitative results obtained here to more realistic situations, involving waves originating in physical sources. In the absence of more realistic exact solutions, however, the solutions described here form an important first step in an understanding of the non-linear interaction that occurs between waves in Einstein’s theory.

2

ELEMENTS OF GENERAL RELATIVITY

It is not the purpose of this chapter to introduce or explain Einstein’s general theory of relativity, since the reader who is not already familiar with it is unlikely to gain much from this book. The main purpose here is simply to clarify the notation that will be used. It is also appropriate in this chapter to briefly introduce the Newman-Penrose formalism which facilitates the geometrical analysis of the colliding plane wave problem and which will be used in Chapter 6 to derive the field equations.

2.1 Basic notation

Basically, we will be following a very traditional approach, and the notation adopted will be that of the well known paper of Newman and Penrose (1962).

Accordingly, a space-time will be represented by a connected C^∞ Hausdorff manifold M together with a locally Lorentz metric g_μv with signature (+, −, −, −) and a symmetric linear connection Г^λ_μv. Greek indices are used to indicate the values 0,1,2,3, and the covariant derivative of a vector is given by

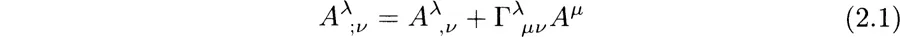
where a comma denotes a partial derivative.

The curvature tensor is given in terms of the connection by

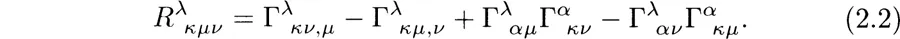
The Ricci tensor, which is the first contraction of the curvature tensor, is given by

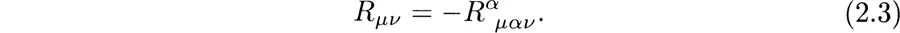
The curvature tensor has twenty independent components. These can be considered as the ten independent components of the Ricci tensor, and the ten independent components of the Weyl tensor, which is the trace free part of the curvature tensor, and is given by

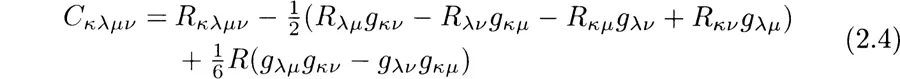
where R = R_α^α is the curvature scalar.

These two groups of components have different physical interpretations. The components of the Ricci tensor are related to the energy-momentum tensor T_μv of the matter field present, through Einstein’s equation

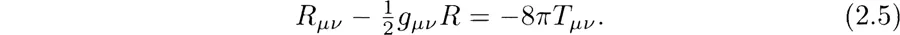
These components can be considered to define the amount of curvature that is directly generated by the matter fields that are...

Table of contents

• Cover
• Title Page
• Copyright Page
• Dedication
• Preface
• Contents
• 1 Introduction
• 2 Elements of General Relativity
• 3 Colliding Impulsive Gravitational Waves
• 4 Plane Waves
• 5 Geometrical Considerations
• 6 The Field Equations
• 7 Boundary Conditions
• 8 Singularity Structure
• 9 The Szekeres Class of Vacuum Solutions
• 10 Other Vacuum Solutions With Aligned Polarization
• 11 Ernst’S Equation for Colliding Gravitational Waves
• 12 Solution-Generating Techniques
• 13 Vacuum Solutions with Non-Aligned Polarization
• 14 The Initial Value Problem
• 15 Colliding Electromagnetic Waves: the Bell–Szekeres Solution
• 16 Ernst’S Equation for Colliding Electromagnetic Waves
• 17 Colliding Electromagnetic Waves: Exact Solutions
• 18 Colliding Electromagnetic Waves: Diagonal Solutions
• 19 Electromagnetic Waves Colliding With Gravitational Waves
• 20 Other Sources
• 21 Related Results
• 22 Conclusions and Prospects
• Appendix: Coordinate Systems
• References
• Index
• Postscript