Logic: The Theory of Formal Inference

Alice Ambrose, Morris Lazerowitz, Morris Lazerowitz

• Publisher: Dover Publications
• Year: 2015
• Print ISBN: 9780486796772
• eBook ISBN: 9780486808598
• Topic: Philosophy
• Subtopic: Logic in Mathematics

Geared toward college undergraduates new to the subject, this concise introduction to formal logic was written by Alice Ambrose and Morris Lazerowitz, a pair of noted scholars and prolific authors in this field. A preliminary section opens the subject under the heading of truth-functions. Two subsequent parts on quantification and classes, each subdivided into numerous brief specifics, complete the overview.
Suitable for students of philosophy as well as mathematics, the three-part treatment begins with the intuitive development of the standard theory of sentential connectives (called "operators"). The theory is further developed with the assistance of truth-tables and ultimately as a logistic system. Part II explores first-order quantification theory. In addition to examining most of the familiar laws that can be expressed by monadic formulas, the text addresses polyadic principles and the theories of identity and descriptions. Part III focuses on elementary concepts of classes, from class membership and class inclusion to the algebra of classes. Each part concludes with a series of exercises.

[ II ]

Quantification

Inferences which are made in terms of the ideas discussed in Part I do not exhaust all possible inferences. The following inferences will readily be seen to be formal, and they involve further terms not definable by our earlier terms. Given the premises

If anyone is a gambler, then he likes to handle money

and

There is someone who is a gambler and is not avaricious,

we may infer the conclusion

There is someone who is not avaricious but likes to handle money.

And from the single premise,

Some even numbers are less than every number greater than the smallest odd prime,

we may infer

It is not the case that for every even number x there is a number which is greater than the smallest odd prime and not greater than x.

An examination of these two deductions makes it clear that their validity hinges on more than just the terms “~”, “⊃”, etc. The terms “any”, “every”, “there is”, “some” also play a role, and are terms which occur as parts of formal statement-forms, i.e., they are themselves formal terms. In fact “every” and “some” were used in Part I, but not in an explicit way. Saying that “q. ⊃ .p ⊃ q” has universal validity and that “~q ⊃ · p ⊃ q” does not are other ways of saying, without explicitly heralding the terms “every” and “some”, that every substitution on “p” and “q” in “q · ⊃ · p ⊃ q” yields a truth, and that some substitutions on “~q ⊃ · p ⊃ q” do not yield truths. But there is an important difference between the use of these terms in connection with the statement-forms explicated in Part I and their use in the above two examples. In “for every p, q, q · ⊃ .p ⊃ q” and in “for some p, q, ~q · p ⊃ q”, “every” and “some” operate on terms within statement-forms which are themselves statement-forms, whereas in the above two examples the terms within the statement-forms on which they operate are not themselves statement-forms. Of these terms no mention either explicit or implicit has yet been made. How the operators “every”, “any”, “some”, called quantifiers, function remains to be explained.

The Universal Quantifier

Compare the statements

If Vladimir is a gambler, then Vladimir likes to handle money

If anyone is a gambler, he likes to handle money.

The difference between them is obviously one of generality. The second is a generalization of which the first is a concrete instance. How the two are related can best be seen by replacing the proper name in the first by a row of dots, to obtain

If … is a gambler, then … likes to handle money.

The components of this form, “… is a gambler”, “… likes to handle money”, are statement-forms, although not formal ones; and they are not truth-functions. If the non-formal terms “gambler” and “likes to handle money” are deleted, the result is a statement-form made up of statement-forms the components of which are not statement-forms. In fact we have arrived at a kind of formula which uses two new and different types of variables, called individual variables and predicate or functional variables. The formula “... is-----” is a form possessed in common by a whole assemblage of statements :

Vladimir is a gambler

Jones is avaricious

Pascal is a mystic.

The standard convention for representing the form of these is to use the letters “x”, “y”, “z”, ... as individual variables and “f”, “g”, “h”, ... as functional variables. The formula “... is - - -” becomes “x is f”, which is written

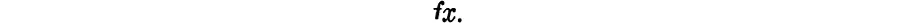
Writing the form of “Vladimir is a gambler” as “fx” and of “Vladimir likes to handle money” as “gx”, the form of “If Vladimir is a gambler, then Vladimir (is a person who) likes to handle money” becomes

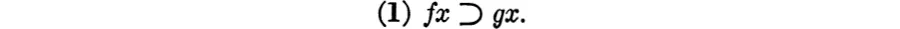
The form of “If anyone is a gambler, then he likes to handle money” can now be seen to be a generalization on the same formula, (1), of which “If Vladimir is a gambler, he likes to handle money” is an instance or specification. The generalization is (1) prefaced by the so-called universal quantifier “(x)”, and written

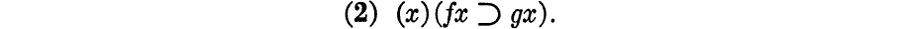
In (1) the variable “x” (and also “f” and “q”) is not prefaced by a quantifier and is said to be free. Given that “f” and “q” are fixed, substitutions made on “x” will yield a variety of statements. In (2), however, “x” is quantified and is said to be bound. No substitutions may be made on “x” when “x” is quantified.

The statements of the following list are taken by logicians to be equivalent in import to “If anyone is a gambler, he likes to handle money”, and therefore are counted as exemplifying formula (2) :

For any x, if z is a g...

Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• I. Truth-Functions
• II. Quantification
• III. Classes