Applications of Green's Functions in Science and Engineering

Michael D. Greenberg

• Publisher: Dover Publications
• Year: 2015
• eBook ISBN: 9780486805849
• Edition: 1
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

Concise and highly regarded, this treatment of Green's functions and their applications in science and engineering is geared toward undergraduate and graduate students with only a moderate background in ordinary differential equations and partial differential equations. The text also includes a wealth of information of a more general nature on boundary value problems, generalized functions, eigenfunction expansions, partial differential equations, and acoustics.
The two-part treatment begins with an overview of applications to ordinary differential equations. Topics include the adjoint operator, delta function, the Green's function method, and the eigenfunction method. The second part, which explores applications to partial differential equations, covers functions for the Laplace, Helmholtz, diffusion, and wave operators. A full index, exercises, suggested reading list, a new preface, and a new brief errata list round out the text.

APPLICATIONS OF GREEN’S FUNCTIONS IN SCIENCE AND ENGINEERING

1. INTRODUCTION

In PART I we will be concerned with the solution of the ordinary differential equation

over an interval a ≤ x ≤ b, subject to certain boundary conditions, where L is an nth order linear ordinary differential operator. By linear, we mean L is such that

for arbitrary constants α, β and any functions ν, w which are at least sufficiently differentiable for L ν and L w to exist.¹ We state, without proof, that L must therefore be of the form

It is easily verified that this does in fact satisfy the linearity requirement (1.2).

By contrast, let us consider a differential operator which is not of the form (1.3); for example,

where we denote d( )/dx = ( )′ for brevity. Applying N to an arbitrary linear combination αν + βw we have

Clearly, the quantity inside the last square brackets is not identically zero for all allowable α’s, β’s, ν’s and w’s, so that N does not satisfy the fundamental requirement (1.2), and is therefore nonlinear. This, of course, is no great surprise since N is clearly not of the form (1.3).

Now let us consider the boundary conditions associated with (1.1). Since L is of nth order, there will be n such conditions of the general form²

where the c_j‘s are given constants, and the B_j‘s are prescribed functionals³ of the unknown u. More specifically, we will limit our attention throughout to B_j‘s which are linear combinations of u and its derivatives, through order n – 1, at the two endpoints a, b. For n = 2, for example, we have

We say that they are linear functionals, because

for arbitrary constants α, β and functions ν, w.

Now, thus far we have discussed both the differential operator L, and the boundary conditions B_j which determine the domain of L and hence complete the specification of the operator. (Note that we distinguish between the term differential operator, which refers to L alone, and the term operator,

say, which refers to L plus the B_j, boundary conditions.⁴) We have been careful to require that both L and the B_j‘s be linear. This is of crucial importance here, since it implies the validity of superposition, which will be basic to the Green’s function method.

FIGURE 1.1 Domain and range of a function f.

To illustrate the idea of superposition, consider, for example, the second order system...

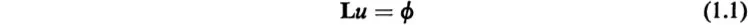
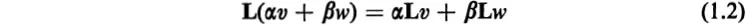
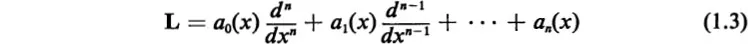
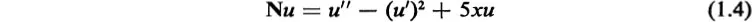
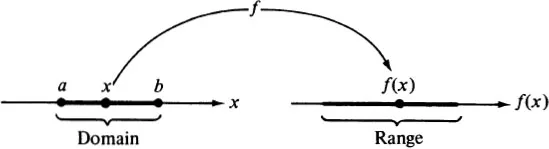
Table of contents

• Cover Page
• Title Page
• Copyright Page
• Dedication
• Preface
• Contents
• Part I: Application to Ordinary Differential Equations
• PART II: Application to Partial Differential Equations
• Errata
• Suggested Reading
• Index