Differential Forms with Applications to the Physical Sciences

Harley Flanders

• Publisher: Dover Publications
• Year: 2012
• ISBN:
  9780486139616
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

"To the reader who wishes to obtain a bird's-eye view of the theory of differential forms with applications to other branches of pure mathematics, applied mathematic and physics, I can recommend no better book." — T. J. Willmore, London Mathematical Society Journal.
This excellent text introduces the use of exterior differential forms as a powerful tool in the analysis of a variety of mathematical problems in the physical and engineering sciences. Requiring familiarity with several variable calculus and some knowledge of linear algebra and set theory, it is directed primarily to engineers and physical scientists, but it has also been used successfully to introduce modern differential geometry to students in mathematics.
Chapter I introduces exterior differential forms and their comparisons with tensors. The next three chapters take up exterior algebra, the exterior derivative and their applications. Chapter V discusses manifolds and integration, and Chapter VI covers applications in Euclidean space. The last three chapters explore applications to differential equations, differential geometry, and group theory.
"The book is very readable, indeed, enjoyable — and, although addressed to engineers and scientists, should be not at all inaccessible to or inappropriate for... first year graduate students and bright undergraduates." — F. E. J. Linton, Wesleyan University, American Mathematical Monthly.

VIII

Applications to Differential Geometry

8.1. Surfaces (Continued)

Everything in this section will be based on the local theory of Section 4.5. Now we have integration at our disposal and we shall discuss a few global results. Let

be a closed surface in E³. For e³ we take the outward drawn normal to

. The mapping

x → e³

is a map on

to the unit sphere S². As x varies over

, e₃ varies over S² a whole number of times, called the degree of the normal map (cf. Section 6.2). The element of area of the normal map is

ω₁ω₂ = Kσ₁σ₂

since

de₃ = ω₁e₁ + ω₂e₂.

Here K is the Gaussian curvature. Hence

where n is the degree. The factor 4π is simply the area of the unit sphere.

In particular, if

is a closed convex surface, then e₃ covers S² exactly once as x covers

, hence

in this case.

After this, we shall limit our discussion to closed convex surfaces. Two important invariants are the total area

and the integrated mean curvature

Given a closed convex surface

and a fixed positive number a, we form the surface

’ parallel to

at distance a by marking off on the outward-drawn normal at each point x of

the distance a and taking the locus of all points so obtained. Thus the typical point on the parallel surface is

y = x + ae₃

where e₃ always denotes the normal at x. We have

It follows that the normal to the parallel sur...

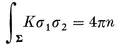
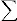
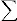
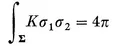
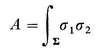
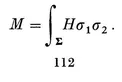
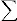
Table of contents

• Title Page
• Copyright Page
• Dedication
• Foreword
• Preface to the Dover Edition
• Preface to the First Edition
• Table of Contents
• I - Introduction
• II - Exterior Algebra
• III - The Exterior Derivative
• IV - Applications
• V - Manifolds and Integration
• VI - Applications in Euclidean Space
• VII - Applications to Differential Equations
• VIII - Applications to Differential Geometry
• IX - Applications to Group Theory
• X - Applications to Physics
• Bibliography
• Glossary of Notation
• Index