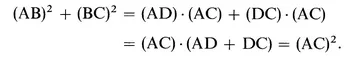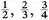A Profile of Mathematical Logic

Howard DeLong

• Publisher: Dover Publications
• Year: 2012
• ISBN:
  9780486139159
• Topic: Mathematics
• Subtopic: Logic in Mathematics
• Index: Mathematics

Anyone seeking a readable and relatively brief guide to logic can do no better than this classic introduction. A treat for both the intellect and the imagination, it profiles the development of logic from ancient to modern times and compellingly examines the nature of logic and its philosophical implications. No prior knowledge of logic is necessary; readers need only an acquaintance with high school mathematics. The author emphasizes understanding, rather than technique, and focuses on such topics as the historical reasons for the formation of Aristotelian logic, the rise of mathematical logic after more than 2,000 years of traditional logic, the nature of the formal axiomatic method and the reasons for its use, and the main results of metatheory and their philosophic import. The treatment of the Gödel metatheorems is especially detailed and clear, and answers to the problems appear at the end.

CHAPTER 1

HISTORICAL BACKGROUND OF MATHEMATICAL LOGIC

§1 INTRODUCTION

Near the end of a work now called Sophistical Refutations, Aristotle apparently claims to have created the subject of logic [1928 183b 34ff].¹ The nearest analog of such a claim in our century is no doubt Freud’s statement in 1914 that “. . . psychoanalysis is my creation; I was for ten years the only person who concerned himself with it...” [1953 7]. It seems probable that Aristotle’s claim is as true as Freud’s. Although Freud’s claim is correct, it is nevertheless possible for the historian to find all kinds of hints and anticipations of psychoanalysis in the works of earlier thinkers; so if the works of Aristotle’s predecessors were all intact, historians could no doubt perform a similar feat.

For example, Plato makes the following statement in the Republic: “The same thing cannot ever act or be acted upon in two opposite ways, or be two opposite things, at the same time, in respect of the same part of itself, and in relation to the same object” [1955 133 (436B)]. Aristotle claims that the most certain of all principles is that “the same attribute cannot at the same time belong and not belong to the same subject and in the same respect” [1928a 1005b 18ff]. This latter principle is Aristotle’s formulation of the Law of Non-Contradiction, and it is tempting to say that Aristotle received not only this law, but many of his ideas on logic, from his predecessors. Nevertheless, one should resist this temptation because Plato makes this remark only in passing and there is no evidence that he, or anyone else before Aristotle, attempted to codify the rules of correct inference. Thus we may accept Aristotle’s claim and ask what led him to create the subject of logic.

“All men by nature desire to know,” Aristotle tells us in the famous opening sentence of the Metaphysics. Both he and Plato believed that philosophy begins in wonder, and there can be little doubt that this motive was strong in Aristotle’s logical investigations. Yet it does not seem that this was the only or even the most pressing motive. Rather two other related but more practical aims were involved, one having to do with mathematics and the other with sophisms. If we wish to know what logic is all about we can do no better than to begin by asking about ancient Greek mathematics before Aristotle.

§2 MATHEMATICS BEFORE ARISTOTLE

The first Greek mathematician was Thales of Miletus (c.624—c.545 B.C.). Thales had visited Egypt and it is probable that he acquired some practical geometrical knowledge there. However, from what we now know of ancient Egyptian mathematics, it seems more likely that anything of value that the Greeks inherited in geometry they received ultimately from ancient Mesopotamia. The latter’s geometric knowledge was vastly superior to Egypt’s. If we can believe tradition, Thales must have been a very great mathematician indeed because he apparently was the first person both to conceive of general geometric propositions and to see the necessity of proving them. A number of geometric propositions are ascribed to him—for example, that the angles at the base of an isosceles triangle are equal—but unfortunately we do not have any idea how he proved them. The same must also be said for Pythagoras (c.566–c.497 B.C.), who according to tradition also visited Egypt and was a pupil of Thales. Pythagoras’ most important contribution to Greek geometry is perhaps best summarized by Proclus (410-485 A.D.), who stated that after Thales, “Pythagoras transformed the study of geometry into a liberal education, examining the principles of the science from the beginning and proving the theorems in an immaterial and intellectual manner . . .” [quoted in Heath 1921 I 141]. If this be true, all the other mathematical achievements (real or alleged) of Thales and Pythagoras are insignificant by comparison, for it would mean that they were chiefly responsible for transforming geometry from an empirical and approximate science into a nonempirical and exact one. We do not, however, know enough to make this claim for them with any kind of assurance.

In any case Pythagoras, who was probably born in Samos, moved to the Greek city of Croton in southern Italy. There he formed a religious brotherhood based on numerous ascetic practices and beliefs. The members apparently believed in the transmigration of souls and in numerology. The specifics of the doctrine are obscure in part because the followers were pledged to secrecy. Although the achievements of Pythagoras are uncertain, it is likely that his order had followers for over a century, and its doctrines certainly influenced many important thinkers, including Plato and Aristotle.

One of the achievements of the school—perhaps even one of Pythagoras’ achievements—was the first proof of the Pythagorean theorem, that is, the theorem which states that the sum of the squares of the sides of a right triangle is equal to the square of the hypotenuse. The truth of the theorem is not very difficult to see—especially in some of its special cases—and either it or some special case of it was discovered independently in a number of cultures, for example in Babylonia, India, and China. We do not know how the Pythagoreans proved the theorem. However, it seems probable that the person who was offering the proof would draw a diagram while speaking and would ask the person listening to the proof if he agreed as he went along. This is the procedure of Socrates in Plato’s Meno (c.390 B.C.), where a special case of the theorem is in fact proved. It also seems likely, as often happens in mathematics, that special cases were proved first and later generalized. Finally, it is probable that the assumptions of the proof were not first stated but were appealed to in the course of the proof, and—sometimes, at least—were not clearly understood by either party of the proof. Supposing all this, we might consider the following a likely story.

Figure 1

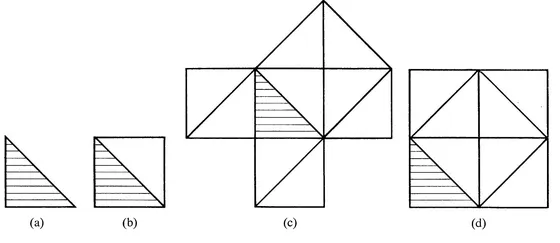
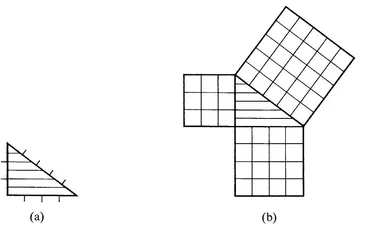
Pythagoras started with an isosceles right triangle (as shown in Fig. 1a) and made a construction on that triangle (Fig. 1b and c). The proof of the theorem can then be given by the process of counting the congruent triangles. Alternatively, he may have constructed one figure (Fig. 1d) and argued only after the construction. There is also evidence to suggest that he (like the ancient Babylonians who preceded him by 1200 years) knew that a 3, 4, 5 triangle is right. If so, he may have made constructions like those in Fig. 2, where it is possible to count unit squares.

Figure 2

Problem 1.² Construct a square seven units by seven units, analogous to Fig. 1(d), such that the theorem’s truth for a 3, 4, 5 triangle can be seen without any further construction.

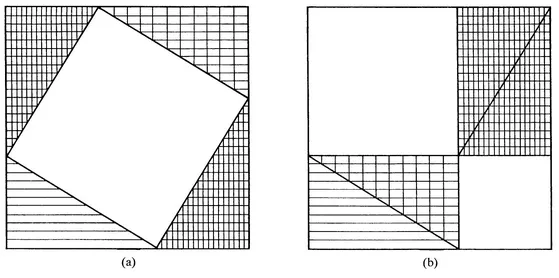
If he proved the theorem in its full generality, he may have used a construction such as that given in Fig. 3(a). It is obvious that any right-angled triangle can be duplicated four times, as indicated in the figure. Now the area of the square of the hypotenuse is equal to the total area of the square minus the area of the four congruent triangles. Rearrange the triangles as indicated in Fig. 3(b). Clearly the sum of the squares of the two legs of the right triangle is equal to the total area of the square minus the area of the four congruent triangles. This is the most intuitively clear proof of the general Pythagorean theorem that has yet been discovered. But just for this reason it is unlikely that Pythagoras discovered it, since it often happens that the first proof of a theorem is far from the easiest.

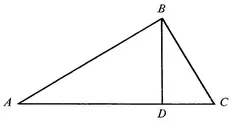
Rather, he probably used his theory of proportion. In modern form this proof could be described by saying that we take triangle ABC (Fig. 4), which is right-angled at B, and drop a perpendicular to the hypotenuse from B.

Figure 3

Figure 4

Now triangles ABC, ADB, BDC are all similar (that is, equiangular) and thus each have sides in the same ratio. Hence

AB : AD : : AC : AB,
BC : DC : : AC : BC.

Re-expressing these relations (by multiplying the means and extremes), we have

(AB)² = (AD) · (AC),
(BC)² = (DC) · (AC).

Adding, we get

When we consider these possible proofs of Pythagoras, a number of features emerge. First, the assumptions are not clearly stated. The appeal at each point is merely to the intuitively obvious. Second, they are meant to be general, ideal, and exact. As Plato puts it,

[students of geometry] make use of visible figures and discourse about them, though what they really have in mind is the originals of which these figures are images: they are not reasoning, for instance, about this particular square or diagonal which they have drawn, but about the Square and the Diagonal; and so in all cases. The diagrams they draw and the models they make are actual things... while the student is seeking to behold those realities which only thought can apprehend [1955 225 (510 D, E)].

Third, no special notation was used. Except in Fig. 4, where the explanation would have become very long without it, only line shading was used, and Pythagoras may have used a similar device. However, he may not have known of the familiar device of labeling triangles with letters, as used in Fig. 4. This might seem utterly unimportant, but we know today that advances in science and mathematics have very often depended on advances in notation. Up to a point they seem merely a matter of convenience, but beyond this the notation itself serves the heuristic function of suggesting further developments of a substantive nature and of allowing a compactness of expression which makes understanding possible. We do not know who first thought of this simple device for naming points, lines, triangles, etc., but without it Euclid’s Elements would not have been possible.

But the Pythagorean relation was not the most important mathematical theorem discovered by Pythagoras and his school; rather it was the discovery and proof of the existence of incommensurate lengths. Commensurate means having a common measure, and it is obvious that the unit is the common measure of all numbers; in fact, a number was understood as a multitude of units [cf. Euclid 1926 II 277]. The arithmetic unit was thought to be indivisible. Fractions such as

, etc., were not understood as representing a part of a unit, but always as 1 unit out of 2, 2 out of 3, 3 out of 4, etc. Given this arithmetic, it was probably obvious that there had to be an indivisible geometric entity so small that any length would be an even multiple of it. It would then follow that every two lengths would be in a definite fixed proportion to each other. What was meant by definite fixed proportion was that the relative size of...