An Introduction to Lebesgue Integration and Fourier Series

Howard J. Wilcox, David L. Myers, David L. Myers

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486682938
• eBook ISBN: 9780486137476
• Topic: Mathematics
• Subtopic: Mathematical Analysis
• Index: Mathematics

This book arose out of the authors' desire to present Lebesgue integration and Fourier series on an undergraduate level, since most undergraduate texts do not cover this material or do so in a cursory way. The result is a clear, concise, well-organized introduction to such topics as the Riemann integral, measurable sets, properties of measurable sets, measurable functions, the Lebesgue integral, convergence and the Lebesgue integral, pointwise convergence of Fourier series and other subjects.
The authors not only cover these topics in a useful and thorough way, they have taken pains to motivate the student by keeping the goals of the theory always in sight, justifying each step of the development in terms of those goals. In addition, whenever possible, new concepts are related to concepts already in the student's repertoire.
Finally, to enable readers to test their grasp of the material, the text is supplemented by numerous examples and exercises. Mathematics students as well as students of engineering and science will find here a superb treatment, carefully thought out and well presented , that is ideal for a one semester course. The only prerequisite is a basic knowledge of advanced calculus, including the notions of compactness, continuity, uniform convergence and Riemann integration.

CHAPTER 1

The Riemann Integral

1. Definition of the Riemann Integral

The problem of finding the area of a plane region bounded by vertical lines x = a and x = b, the horizontal line y = 0, and the graph of the non-negative function y = f(x), is a very old one (although, of course, it has not always been stated in this terminology). The Greeks had a method which they applied successfully to simple cases such as f(x) = x². This “method of exhaustion” consisted essentially in approximating the area by figures whose areas were known already—such as rectangles and triangles. Then an appropriate limit was taken to obtain the result.

In the seventeenth century, Newton and Leibnitz independently found an easy method for solving the problem. The area is given by F(b)–F(a), where F is an antiderivative of f. This is the familiar Fundamental Theorem of Calculus; it reduced the problem of finding areas to that of finding antiderivatives.

Eventually mathematicians began to worry about functions not having antiderivatives. When that happened, they were forced to return again to the basic problem of area. At the same time, it became clear that a more precise formulation of the problem was necessary. Exactly what is area, anyway? Or, more generally, how can

be defined rigorously for as wide a class of functions as possible?

In the middle of the nineteenth century, Cauchy and Riemann put the theory of integration on a firm footing. They described—at least theoretically—how to carry out the program of the Greeks for any function f. The result is the definition of what is now called the Riemann integral of f. This is the integral studied in standard calculus courses.

1.1 Definition: A partition P of a closed interval [a,b] is a finite sequence (x₀,x₁, . . . x_n) such that a = x₀ < x₁ < . . . < x_n = b. The norm (or width, or mesh) of P, denoted ||P||, is defìned by

That is, ||P|| is the length of the longest of the subintervals [x₀,x₁], [x_2,x₃]_, . . . , [x_n−1, x_n].

1.2 Definition: Let P = (x₀, . . . ,x_n) be a partition of [a,b], and let f be defined on [a,b]. For each i = 1, . . . ,n, let x_i* be an arbitrary point in the interval [x_i−1,x_i]. Then any sum of the form

is called a Riemann sum of f relative to P.

Notice that R(f,P) is not completely d...

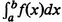
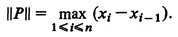
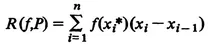
Table of contents

• Title Page
• Copyright Page
• Table of Contents
• Preface
• CHAPTER 1 - The Riemann Integral
• CHAPTER 2 - Measurable Sets
• CHAPTER3 - Properties of Measurable Sets
• CHAPTER 4 - Measurable Functions
• CHAPTER 5 - The Lebesgue Integral
• CHAPTER6 - Convergence and The Lebesgue Integral
• CHAPTER7 - Function Spaces and L2
• CHAPTER 8 - The L2 Theory of Fourier Series
• CHAPTER 9 - Pointwise Convergence of Fourier Series
• Appendix
• Bibliography
• INDEX
• A CATALOG OF SELECTED DOVER BOOKS IN SCIENCE AND MATHEMATICS
• CATALOG OF DOVER BOOKS