The Theory of Spinors

Élie Cartan

• Publisher: Dover Publications
• Year: 2012
• eBook ISBN: 9780486137322
• Topic: Mathematics
• Subtopic: Topology
• Index: Mathematics

The French mathematician Élie Cartan (1869–1951) was one of the founders of the modern theory of Lie groups, a subject of central importance in mathematics and also one with many applications. In this volume, he describes the orthogonal groups, either with real or complex parameters including reflections, and also the related groups with indefinite metrics. He develops the theory of spinors (he discovered the general mathematical form of spinors in 1913) systematically by giving a purely geometrical definition of these mathematical entities; this geometrical origin makes it very easy to introduce spinors into Riemannian geometry, and particularly to apply the idea of parallel transport to these geometrical entities.
The book is divided into two parts. The first is devoted to generalities on the group of rotations in n-dimensional space and on the linear representations of groups, and to the theory of spinors in three-dimensional space. Finally, the linear representations of the group of rotations in that space (of particular importance to quantum mechanics) are also examined. The second part is devoted to the theory of spinors in spaces of any number of dimensions, and particularly in the space of special relativity (Minkowski space). While the basic orientation of the book as a whole is mathematical, physicists will be especially interested in the final chapters treating the applications of spinors in the rotation and Lorentz groups. In this connection, Cartan shows how to derive the "Dirac" equation for any group, and extends the equation to general relativity.
One of the greatest mathematicians of the 20th century, Cartan made notable contributions in mathematical physics, differential geometry, and group theory. Although a profound theorist, he was able to explain difficult concepts with clarity and simplicity. In this detailed, explicit treatise, mathematicians specializing in quantum mechanics will find his lucid approach a great value.

PART I

Spinors in three-dimensional space Linear representations of the group of rotations

CHAPTER I

n-DIMENSIONAL EUCLIDEAN SPACE; ROTATIONS AND REVERSALS

I. EUCLIDEAN SPACE

1. Definition; Vectors

Points in n-dimensional Euclidean space may be defined as sets of n numbers (x₁, x₂, . . . , x_n), the square of the distance from a point (x) to the origin (0, 0,..., 0) being given by the fundamental form

(1)

this expression also represents the scalar square or the square of the length of the vector x drawn from the origin to the point (x); the n quantities x, are called the components of this vector. The co-ordinates x₁ may be arbitrary complex numbers, and it is then said that the Euclidean space is complex; but if they are all real, we have real Euclidean space. In the real domain there also exists pseudo-Euclidean spaces, each corresponding to a real non-positive definite fundamental form

(2)

we shall assume, without any loss of generality, that n − h ≥ h.

In real spaces, we are led to consider vectors whose components are not all real; such vectors are said to be complex.

A vector is said to be isotropic if its scalar square is zero, that is to say if its components make the fundamental form equal to zero. A vector in real or complex Euclidean space is said to be a unit vector if its scalar square equals 1. In real pseudo-Euclidean space whose fundamental form is not positive definite, a distinction is made between real space-like vectors which have positive fundamental forms, and real time-like vectors which have negative fundamental forms; a space-like unit vector has a fundamental form equal to + 1, for a time-like unit vector it equals −1.

If we consider two vectors x, y, and the vector x + λy, where λ is a given parameter, that is to say the vector with components x, + λy_i, the scalar square of this vector is

x² + λ²y² + 2λx.y,

where x.y is defined as the sum x₁y₁ + x₂y₂ + ... + x_ny_n. This sum is the scalar product of the two vectors; in the case of a pseudo-Euclidean space, the scalar product is

x₁y₁ + x₂y₂ + . . . + x_n−hy_n−h − x_n−h+1y_n−h+1 − ... − x_ny_n.

Two vectors are said to be orthogonal, or perpendicular to each other, if their scalar product is zero; an isotropic vector is perpendicular to itself. The space of the vectors orthogonal to a given vector is a hyperplane of n − 1 dimensions (defined by a linear equation in the co-ordinates).

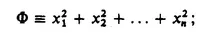
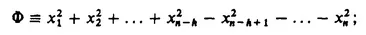
2. Cartesian frames of reference

The n vectors e₁, e₂, e₃ e_n, whose components are all zero except one which is equal to 1, constitute a basis, in the sense that every vector x is a linear combination x₁e₁ + x₂e₂ + ... + x_ne_n of these n vectors. These basis vectors are orthogonal in pairs; they constitute what we shall call an orthogonal Cartesian frame of reference.

More generally, let us take n li...

Table of contents

• DOVER BOOKS ON MATHEMATICS
• Title Page
• Copyright Page
• FOREWORD
• INTRODUCTION
• Table of Contents
• PART I - Spinors in three-dimensional space Linear representations of the group of rotations
• PART II - SPINORS IN SPACE OF N > 3 DIMENSIONS SPINORS IN RIEMANNIAN GEOMETRY
• BIBLIOGRAPHY
• SUBJECT INDEX
• A CATALOG OF SELECTED DOVER BOOKS IN SCIENCE AND MATHEMATICS