Concepts of Mathematical Modeling

Walter J. Meyer

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486435152
• eBook ISBN: 9780486137247
• Topic: Mathematics
• Subtopic: Mathematical Analysis
• Index: Mathematics

Appropriate for undergraduate and graduate students, this text features independent sections that illustrate the most important principles of mathematical modeling, a variety of applications, and classic models. Students with a solid background in calculus and some knowledge of probability and matrix theory will find the material entirely accessible. The range of subjects includes topics from the physical, biological, and social sciences, as well as those of operations research. Discussions cover related mathematical tools and the historical eras from which the applications are drawn. Each section is preceded by an abstract and statement of prerequisites, and answers or hints are provided for selected exercises. 1984 edition.

CHAPTER ONE

THE SCOPE OF MATHEMATICAL MODELING

1 MODELS, MATHEMATICAL AND OTHERWISE

Abstract This section introduces the concepts of mathematical and nonmathematical models in a nontechnical way. Our examples show that mathematical models are often, but not always, better; that nonmathematical models may evolve into mathematical ones; and that experimental work may be needed to provide data for mathematical models.

Prerequisites None.

No human investigation can claim to be scientific if it doesn’t pass the test of mathematical proof.

Leonardo Da Vinci

Mathematical modeling is an attempt to describe some part of the real world in mathematical terms. It is an endeavor as old as antiquity but as modern as tomorrow’s newspaper. It has led to some good mathematical models and some bad ones, which are best forgotten. Sometimes mathematical models have been welcomed with great enthusiasm—even when their value was uncertain or negligible; other times good mathematical models have been greeted with indifference, hostility, or ridicule. Mathematical models have been built in the physical, biological, and social sciences. The building blocks for these models have been taken from calculus, algebra, geometry, and nearly every other field within mathematics.

In short, mathematical modeling is a rich and diverse activity with many interesting aspects. The aim of this book is to display by examples some of the many facets of mathematical modeling.

But before we plunge into this, it seems only fair to say something about models of a nonmathematical nature. In ordinary language the word “model” has many meanings. What we will mean by it is this.

Definition

A model is an object or concept that is used to represent something else. It is reality scaled down and converted to a form we can comprehend.

For example, a model airplane, made of wood, plastic, and glue, is a model of a real airplane. Another example is the idea that, in politics, public opinion is like a pendulum because it changes periodically from left- to right-wing ideas then back again in a way which reminds us of a pendulum swinging back and forth. In our terminology we would say that a pendulum is a model for public opinion.

A model aiplane and pendulum are physical objects; so they are not mathematical models.

Definition

A mathematical model is a model whose parts are mathematical concepts, such as constants, variables, functions, equations, inequalities, etc.

Example 1 that follows illustrates the differences between mathematical and nonmathematical models. In this example the mathematical model is, in many ways, superior to its nonmathematical counterpart. The other examples in this section also illustrate the great value of mathematical models. But we shall see that nonmathematical models have value as well. Among other things, they often stimulate the development of mathematical models.

Example 1 Aircraft Flight

To find out how an aircraft will behave in flight, we could make a physical model of the aircraft and test it under various weather conditions. There are a great many things one might want to know: Is the plane stable in the air? How fast can it go? How steeply can it climb? Etc. To focus our discussion, let’s consider the question of how great the lift force on the plane is when it takes off.

The lift force is the force pushing up on the wings. This force is largely what determines how steeply the plane can climb. If we did experiments with a physical model, we could find out almost anything we wanted to know about it. For example, we could discover that the lift force was dependent on how fast the plane was moving. By flying the plane at different speeds, we could make a table of values relating lift force to velocity and a graph of this table of values that might look like Figure 1.

Figure 1 Points are plotted from a table of values obtained from wind-tunnel experiments. The different points represent trials at different speeds.

But there is an entirely different approach to this problem, one based on a mathematical model. This mathematical model consists of a single equation which relates the lift force to other factors. It is

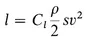
(1)

where l = lift force

C_l = a certain numerical value called the lift coefficient whose exact value depends on the shape of the plane

ρ = density of the air

v = velocity of the plane

s = total surface area of the tops of the wings

We can estimate s from the blueprints of the plane we propose to build. ρ is a measurement we can make in the atmosphere. (It may differ a little from one airport to another.) C_l is a number which differs from plane to plane and is a little hard to estimate for a plane that has not yet been built and tested. But there are methods that yield reasonable estimates; so let’s assume C_l, is known. Then the product C_l(ρ/2)s in Equation (1) becomes a known constant. If we call this constant a, then Equation (1) becomes an equation linking only two variables, l and v:

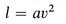
(2)

Using this equation, we can generate the graph shown in Figure 2 with a moment’s worth of calcul...

Table of contents

• Title Page
• Dedication
• Copyright Page
• Table of Contents
• PREFACE
• CHAPTER ONE - THE SCOPE OF MATHEMATICAL MODELING
• CHAPTER TWO - THE RELATION OF MODELS TO DATA
• CHAPTER THREE - EVALUATION OF MATHEMATICAL MODELS
• CHAPTER FOUR - OPTIMIZATION
• CHAPTER FIVE - CHOOSING THE MATHEMATICS FOR THE MODEL
• APPENDIX - DIFFERENTIAL EQUATIONS
• ANSWERS TO SELECTED EXERCISES
• INDEX