Nonlinear Mechanics

A Supplement to Theoretical Mechanics of Particles and Continua

Alexander L. Fetter, John Dirk Walecka

• Publisher: Dover Publications
• Year: 2012
• ISBN:
  9780486136998
• Topic: Physical Sciences
• Subtopic: Physics
• Index: Physics

In their prior Dover book, Theoretical Mechanics of Particles and Continua, Alexander L. Fetter and John Dirk Walecka provided a lucid and self-contained account of classical mechanics, together with appropriate mathematical methods. This supplement—an update of that volume—offers a bridge to contemporary mechanics.
The original book's focus on continuum mechanics—with chapters on sound waves in fluids, surface waves on fluids, heat conduction, and viscous fluids—forms the basis for this supplement's discussion of nonlinear continuous systems. Topics include linearized stability analysis; a detailed examination of the Rayleigh-Bénard problem, from its formulation to issues of linearized theory of convective instability and expansion in Fourier modes; and the direct derivation of Lorenz equations for simple physical configuration. The first half of the original text deals with particle mechanics, and this supplement returns to the study of systems with a finite number of degrees of freedom. A concluding section presents a series of problems that reinforce the supplement's teachings.

Part I

Introduction

1 Motivation

The book Theoretical Mechanics of Particles and Continua was originally published by McGraw-Hill Book Co. in 1980 [Fe80a]. Subsequently, Dover Publications reprinted it in 2003 [Fe03]. The original preface to [Fe80a] states:

We intend this frankly as a textbook and aim to provide a lucid and selfcontained account of classical mechanics, together with appropriate mathematical methods.

Over the years, many colleagues and students have told us how much they liked using this text.

The first section of [Fe80a] starts with the sentence:

Although Newton’s laws of motion are easily stated, their full implications involve subtle and complicated nonlinear phenomena that remain only partially explored.

Since 1980 the advent of powerful inexpensive computers has revolutionized this exploration. Currently anyone with a desktop computer can simply pick appropriate initial conditions and numerically integrate a set of nonlinear ordinary differential equations, or, equivalently, iterate a set of nonlinear finite-difference equations. These numerical investigations have discovered many fascinating and unexpected phenomena, such as chaos and fractals (see, for example, [Za85, Gu90, Mc94, Ot02]). Simultaneously, powerful mathematical methods have been developed to describe nonlinear mechanics (see, for example, [Ar89, Li92, Pe92, Jo98]).

The preface to [Fe03] further states:

We have each taught particle and continuum mechanics many times over the years, both at Stanford and at William and Mary, and enjoyed having this book available as a text.... In the past several times that we have taught the course, each of us has supplemented this material with additional lectures on more modern topics such as nonlinear dynamics, the Lorenz equations, and chaos. We hope that this supplemental material will also be available in published form at some point.

When Dover reprinted the original version [Fe03], the authors considered preparing a revised second edition but decided that it was more valuable to have the text immediately available for the use of students and instructors. Thus arose the idea for a supplement that would provide a bridge from [Fe80a] to contemporary (typically nonlinear) mechanics. We re-emphasize that this material serves as a textbook from which one can learn. Indeed, we claim no originality and are definitely not experts on these topics.

The second half of [Fe80a] focuses on continuum mechanics with chapters on Sound waves in fluids, Surface waves on fluids, Heat conduction, and Viscous fluids. A natural extension is to use this material as a basis for discussing nonlinear continuous systems, which we proceed to do in Part II of this supplement.

The Euler equation for an ideal incompressible fluid simplifies considerably for irrotational flow because the velocity field (a vector) is then derivable from a scalar velocity potential. In this case, the Euler equation can be integrated to yield Bernoulli’s equation. Part II starts with a linearized stability analysis describing two classic physical problems: the onsets of (1) the Rayleigh-Taylor gravitational instability for two fluids with the heavier on top, and (2) the Kelvin-Helmholtz shear instability where the fluids are gravitationally stable but undergo relative transverse motion. This material provides a nice introduction, for it simply amplifies three problems appearing in the original text [Fe80b].¹

The Navier-Stokes equation adds viscosity to the description of these fluids. Typically, a viscous fluid undergoes rotational motion with nonzero vorticity (the curl of the velocity). In addition, the vorticity itself diffuses at a rate determined by the kinematic viscosity. The Navier-Stokes equation is solved for some simple physical configurations in [Fe80a]. Inclusion of heat flow, both conduction and convection, leads to still richer physical phenomena. If the fluid is heated from below, the decrease in density associated with thermal expansion substantially affects the dynamics, and the resulting buoyant force eventually initiates convection. This convective instability of a viscous fluid heated from below is known as the Rayleigh-Bénard problem. The simplest approximation is to retain only the leading linear temperature dependence in the density (known as the Boussinesq approximation). We analyze the resulting set of coupled nonlinear dynamical equations in some detail, obtaining the conditions for the onset of the striking convective roll instability and deducing properties of the linearized solutions (see, for example, [Ch81, La87, Bo00]).

The coupled physical amplitudes that obey the nonlinear Boussinesq equations can be expanded in a complete set of spatial normal modes [Sa62]. If the resulting system of coupled nonlinear equations is truncated to retain only the first two modes, then an appropriate redefinition of variables yields the equations first derived by Lorenz as a model for weather [Lo63, Sp82]. These celebrated and remarkable Lorenz equations constitute a discrete dynamical system with three dependent variables and one control parameter. As we shall see explicitly, their solution mimics the much more complicated Rayleigh-Bénard problem with an infinite number of degrees of freedom. The numerical solution to these three coupled, first-order, nonlinear, ordinary differential equations provided one of the first observations of the phenomenon of chaos. Today, it is a simple matter for students to solve these equations on a desktop computer and investigate their properties. Indeed, this system exemplifies much of what makes modern mechanics so enjoyable and fascinating.

For pedagogical reasons, we take an extended path to the Lorenz equations, exploring some interesting physical phenomena along the way. Part II concludes with a direct derivation based on a simplified physical situation where the low-lying modes indeed decouple and the relevant motion of the fluid is readily observed [Yo85]. Properties of the solutions to the Lorenz equations are analyzed in detail in Part III.

The first half of [Fe80a] deals with particle mechanics, and Part III of this supplement returns to the study of systems with a finite number of degrees of freedom. It begins by introducing the Duffing oscillator. This typical and important nonlinear oscillator augments the familiar quadratic harmonic oscillator potential energy with a quartic term. It exhibits very characteristic behavior (spontaneous symmetry breaking and bifurcation) as the sign of the quadratic term passes through zero (note that this behavior goes well beyond the usual stable harmonic oscillator).

The Duffing oscillator also provides a prelude to the discussion of coupled nonlinear systems. Suppose that the quadratic oscillator potential yields a stable frequency ω₀. If the nonlinear quartic term is small, it is natural to seek a perturbative solution to the equation of motion, expanding in the strength of the quartic term. Unfortunately, the first-order correction has a term that not only oscillates but also increases linearly with t. Such behavior indicates that a resonant driving term leads to a secular growth in the coordinate. This conclusion violates a theorem that the dynamical motion for this problem remains bounded for all t. It indicates that the straightforward perturbative analysis fails when ω₀t ≈ 1. A more powerful improved analysis includes a simultaneous shift in the frequency ω₀ → ω, which eliminates the secular term and allows the perturbative approach to hold for much longer times. This calculation illustrates the importance of resonance in driving the perturbations of nonlinear systems. We present some numerical results for this interesting system.

A different and particularly useful prototype for periodic nonlinear motion is the planar pendulum that is familiar from freshman physics. We initially use the usual dynamical variables (p, q) = (p_θ, θ), with θ the angle measured from the down position and p_θ the angular momentum (Fig. 1.1). The full equations of motion are highly nonlinear. This simple physical system is remarkably rich, for it has both unstable and stable equilibrium points (up and down) and both libration (oscillation) and rotation (over the top) types of motion. It serves to introduce the concept of a fixed point corresponding to stationary coordinates. In addition, the linearized stability analysis about the fixed points leads to the notion of a separatrix formed by an orbit through an unstable fixed point. In this example, the solutions have a qualitatively different character on the two sides of the separatrix. In the elementary analysis, of course, the equations are linearized about the stable fixed point where the pendulum hangs down, and one finds simple harmonic motion. With an additional damping term, the system will decay back to this stable fixed point; in this case the fixed point is known as an attractor.

The action-angle variables (J, φ) will be seen to simplify and unify the dynamics of nonlinear periodic hamiltonian systems. We start by studying such a system with one degree of freedom. For both rotational and librational motion, the action J is a constant, and the angle variable increases linearly with the time. No matter how complicated the dynamics, the dynamical trajectory in this two-dimensional (J, φ) phase space is simply uniform motion along a straight line. As particular and important examples, we develop the action-angle description of the simple harmonic oscillator and the pendulum.

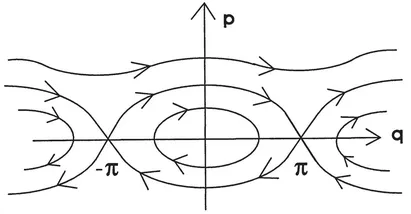
Fig. 1.1. Sketch of phase-space orbits for a simple pendulum with (p, q) = (p_θ, θ). The closed orbits describe stable oscillations (librations); for small displacements, energy conservation implies that they form ellipses. The top orbit is a rotation where the pendulum goes over the top and the angle increases continuously. The origin is a stable fixed point, and the crossing points on the q axis at ±π are unstable fixed points where the pendulum...