Functional Analysis

George Bachman, Lawrence Narici, Lawrence Narici

• Publisher: Dover Publications
• Year: 2012
• eBook ISBN: 9780486136554
• Topic: Mathematics
• Subtopic: Functional Analysis
• Index: Mathematics

Excellent treatment of the subject geared toward students with background in linear algebra, advanced calculus, physics and engineering. Text covers introduction to inner-product spaces, normed and metric spaces, and topological spaces; complete orthonormal sets, the Hahn-Banach theorem and its consequences, spectral notions, square roots, a spectral decomposition theorem, and many other related subjects. Chapters conclude with exercises intended to test and reinforce reader’s understanding of text material. A glossary of definitions, detailed proofs of theorems, bibliography, and index of symbols round out this comprehensive text. 1966 edition.

CHAPTER 1

Introduction to Inner Product Spaces

In this chapter, some of the conventions and terminology that will be adhered to throughout this book will be set down. They are listed only so that there can be no ambiguity when terms such as “vector space” or “linear transformation” are used later, and are not intended as a brief course in linear algebra.

After establishing our rules, certain basic notions pertaining to inner product spaces will be touched upon. In particular, certain inequalities and equalities will be stated. Then a rather natural extension of the notion of orthogonality of vectors from the euclidean plane is defined. Just as choosing a mutually orthogonal basis system of vectors was advantageous in two- or three-dimensional euclidean space, there are also certain advantages in dealing with orthogonal systems in higher dimensional spaces. A result proved in this chapter, known as the Gram-Schmidt process, shows that an orthogonal system of vectors can always be constructed from any denumerable set of linearly independent vectors.

Focusing then more on the finite-dimensional situation, the notion of the adjoint of a linear transformation is introduced and certain of its properties are demonstrated.

1.1 Some Prerequisite Material and Conventions

The most important structure in functional analysis is the vector space (linear space)—a collection of objects, X, and a field F, called vectors and scalars, respectively, such that, to each pair of vectors x and y, there corresponds a third vector x + y, the sum of x and y in such a way that X constitutes an abelian group with respect to this operation. Moreover, to each pair a and x, where a is a scalar and x is a vector, there corresponds a vector ax, called the product of α and x, in such a way that

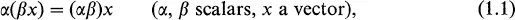
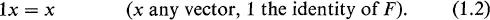
For scalars α, β and vectors x, y, we demand

We shall often describe the above situation by saying that X is a vector space over F and shall rather strictly adhere to using lower-case italic letters (especially x, y, z, …) for vectors and lower-case Greek letters for scalars. The additive identity element of the field will be denoted by 0, and we shall also denote the additive identity element of the vector addition by 0. We feel that no confusion will arise from this practice, however. A third connotation that the symbol 0 will carry will be the transformation of one vector space into another and mapping every vector of the first space into the zero vector of the second.

The multiplicative identity of the field will be denoted by 1 and so will that transformation of a vector space into itself which maps every vector into itself.

A collection of vectors x₁, x₂, …, x_n is said to be linearly independent if the relation

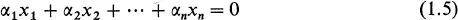
implies that each α_i = 0; in other words, no linear combination of linearly independent vectors whatsoever (nontrivial, of course) can yield the zero vector. An arbitrary collection of vectors is said to be line...

Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• Preface
• CHAPTER 1. Introduction to Inner Product Spaces
• CHAPTER 2. Orthogonal Projections and the Spectral Theorem for Normal Transformations
• CHAPTER 3. Normed Spaces and Metric Spaces
• CHAPTER 4. Isometries and Completion of a Metric Space
• CHAPTER 5. Compactness in Metric Spaces
• CHAPTER 6. Category and Separable Spaces
• CHAPTER 7. Topological Spaces
• CHAPTER 8. Banach Spaces, Equivalent Norms, and Factor Spaces
• CHAPTER 9. Commutative Convergence, Hilbert Spaces, and Bessel’s Inequality
• CHAPTER 10. Complete Orthonormal Sets
• CHAPTER 11. The Hahn-Banach Theorem
• CHAPTER 12. Consequences of the Hahn-Banach Theorem
• CHAPTER 13. The Conjugate Space of C[a, b]
• CHAPTER 14. Weak Convergence and Bounded Linear Transformations
• CHAPTER 15. Convergence in L(X, Y) and the Principle of Uniform Boundedness
• CHAPTER 16. Closed Transformations and the Closed Graph Theorem
• CHAPTER 17. Closures, Conjugate Transformations, and Complete Continuity
• CHAPTER 18. Spectral Notions
• CHAPTER 19. Introduction to Banach Algebras
• CHAPTER 20. Adjoints and Sesquilinear Functionals
• CHAPTER 21. Some Spectral Results for Normal and Completely Continuous Operators
• CHAPTER 22. Orthogonal Projections and Positive Definite Operators
• CHAPTER 23. Square Roots and a Spectral Decomposition Theorem
• CHAPTER 24. Spectral Theorem for Completely Continuous Normal Operators
• CHAPTER 25. Spectral Theorem for Bounded, Self-Adjoint Operators
• CHAPTER 26. A Second Approach to the Spectral Theorem for Bounded, Self-Adjoint Operators
• CHAPTER 27. A Third Approach to the Spectral Theorem for Bounded, Self-Adjoint Operators and Some Consequences
• CHAPTER 28. Spectral Theorem for Bounded, Normal Operators
• CHAPTER 29. Spectral Theorem for Unbounded, Self-Adjoint Operators
• Bibliography
• Index of Symbols
• Subject Index
• Errata