Taxicab Geometry

An Adventure in Non-Euclidean Geometry

Eugene F. Krause

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486252025
• eBook ISBN: 9780486136066
• Topic: Mathematics
• Subtopic: Geometry
• Index: Mathematics

This entertaining, stimulating textbook offers anyone familiar with Euclidean geometry — undergraduate math students, advanced high school students, and puzzle fans of any age — an opportunity to explore taxicab geometry, a simple, non-Euclidean system that helps put Euclidean geometry in sharper perspective.
In taxicab geometry, the shortest distance between two points is not a straight line. Distance is not measured as the crow flies, but as a taxicab travels the "grid" of the city street, from block to block, vertically and horizontally, until the destination is reached. Because of this non-Euclidean method of measuring distance, some familiar geometric figures are transmitted: for example, circles become squares.
However, taxicab geometry has important practical applications. As Professor Krause points out, "While Euclidean geometry appears to be a good model of the 'natural' world, taxicab geometry is a better model of the artificial urban world that man has built."
As a result, the book is replete with practical applications of this non-Euclidean system to urban geometry and urban planning — from deciding the optimum location for a factory or a phone booth, to determining the most efficient routes for a mass transit system.
The underlying emphasis throughout this unique, challenging textbook is on how mathematicians think, and how they apply an apparently theoretical system to the solution of real-world problems.

1 WHAT IS TAXICAB GEOMETRY?

THE USUAL way to describe a (plane) geometry is to tell what its points are, what its lines are, how distance is measured, and how angle measure is determined. When you studied Euclidean coordinate geometry the points were the points of a coordinatized plane. Each of these points could be designated either by a capital letter or by an ordered pair of real numbers (the “coordinates” of the point). For example, in Fig. 1, P = (−2, −1) and Q = (1, 3). The lines were the usual long, straight, skinny sets of points; angles were measured in degrees with a (perfect) protractor; and distances either were measured “as the crow flies” with a (perfect) ruler or were calculated by means of the Pythagorean Theorem.

For example, in Fig. 1 the distance from P to Q could be found by considering a right triangle having

as its hypotenuse. The dotted segments are the legs of one such triangle. (Are there any other such right triangles?) These legs clearly have lengths 3 and 4. Thus, by the Pythagorean Theorem, the Euclidean distance from P to Q is

. We shall use the symbol d_E to represent the Euclidean distance function. Thus, in our example we would write

d_E(P, Q) = 5,

and read it “The Euclidean distance from P to Q is 5.”

Taxicab geometry is very nearly the same as Euclidean coordinate geometry. The points are the same, the lines are the same, and angles are measured in the same way. Only the distance function is different. In Fig. 1 the taxicab distance from P to Q, written d_T(P, Q), is determined not as the crow flies, but instead as a taxicab would drive. We count how many blocks it would have to travel horizontally and vertically to get from P to Q. The dotted segments suggest one taxi route. Clearly

d_T(P, Q) = 7.

“The taxi distance from P to Q is 7.”

Figure 2 is a reminder that most of the points of the coordinate plane do not have two integer coordinates. In the figure a pair of “arbitrary” points A = (a₁, a₂) and B = (b₁, b₂) is given. What are t...

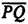
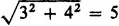
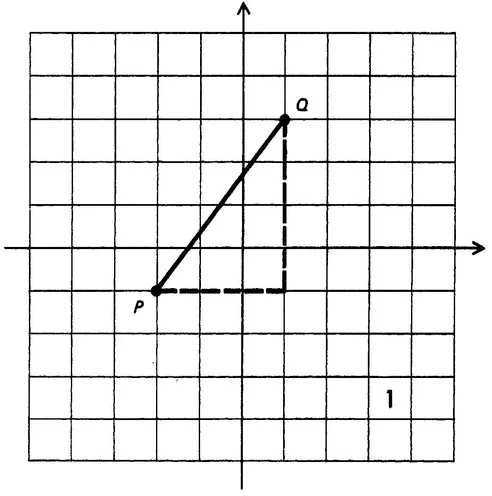
Table of contents

• Dover Science Books
• Title Page
• Copyright Page
• about this book
• about the author
• materials
• TO THE TEACHER
• Table of Contents
• 1 WHAT IS TAXICAB GEOMETRY?
• 2 SOME APPLICATIONS
• 3 SOME GEOMETRIC FIGURES
• 4 DISTANCE FROM A POINT TO A LINE
• 5 TRIANGLES
• 6 FURTHER APPLICATIONS TO URBAN GEOGRAPHY
• 7 SOME DIRECTIONS FOR FURTHER RESEARCH
• APPENDIX - taxicab geometry and euclidean geometry compared
• SELECTED ANSWERS
• INDEX