Geometry of Complex Numbers

Hans Schwerdtfeger

• Publisher: Dover Publications
• Year: 2012
• Print ISBN:
  9780486638300
• eBook ISBN:
  9780486135861
• Topic: Mathematics
• Subtopic: Geometry
• Index: Mathematics

"This book should be in every library, and every expert in classical function theory should be familiar with this material. The author has performed a distinct service by making this material so conveniently accessible in a single book." — Mathematical Review
Since its initial publication in 1962, Professor Schwerdtfeger's illuminating book has been widely praised for generating a deeper understanding of the geometrical theory of analytic functions as well as of the connections between different branches of geometry. Its focus lies in the intersection of geometry, analysis, and algebra, with the exposition generally taking place on a moderately advanced level. Much emphasis, however, has been given to the careful exposition of details and to the development of an adequate algebraic technique.
In three broad chapters, the author clearly and elegantly approaches his subject. The first chapter, Analytic Geometry of Circles, treats such topics as representation of circles by Hermitian matrices, inversion, stereographic projection, and the cross ratio. The second chapter considers in depth the Moebius transformation: its elementary properties, real one-dimensional projectivities, similarity and classification of various kinds, anti-homographies, iteration, and geometrical characterization. The final chapter, Two-Dimensional Non-Euclidean Geometries, discusses subgroups of Moebius transformations, the geometry of a transformation group, hyperbolic geometry, and spherical and elliptic geometry. For this Dover edition, Professor Schwerdtfeger has added four new appendices and a supplementary bibliography.
Advanced undergraduates who possess a working knowledge of the algebra of complex numbers and of the elements of analytical geometry and linear algebra will greatly profit from reading this book. It will also prove a stimulating and thought-provoking book to mathematics professors and teachers.

I

ANALYTIC GEOMETRY OF CIRCLES

§ 1. Representation of circles by hermitian matrices

a. One circle. All points z = x+iy of the complex plane which form the circumference of the circle of radius ρ about the centre γ = α + iβ are characterized by the equation

(x–α)² + (y–β)² = ρ².

Writing the left-hand side as

we obtain the equation of the circle in the form

(1.1)

For our purposes it is advisable to start with the more general equation

(1.2)

where A and D are real, and B and C are conjugate complex numbers. The matrix

(1.21)

is therefore a hermitian matrix.

Evidently the equation (1.1) is a particular case of (1.2). Both equations will represent the same circle if A ≠ 0 and

(1.3)

Every hermitian matrix

is associated with an equation (1.2). We shall say that it defines, or is representative of, a ‘circle’ except if A = B = C = 0. Accordingly the letter

is used to denote both the circle and the corresponding hermitian matrix. Two hermitian matrices

and

₁ represent the same circle if and only if

₁=λ

where λ is a real number different from zero.

In order to distinguish between the different types of ‘circles’ included in this definition we introduce the determinant

(1.4) Δ = |

| = AD–BC = AD–|B|²,

evidently a real number, which is called the discriminant of the circle

. For a real circle as represented by the equation (1.1), Δ = – ρ². For the circle given by the equation (1.2), according to (1.3) the discriminant is found to be equal to

(1.41) Δ = –A²ρ².

Now it is readily seen that the circle

given by the equation (1.2) is an ordinary real circle if and only if A ≠ 0 and Δ < 0. Its centre γ and radius ρ can then be found from (1.3), (1.41), and we shall also denote it by (γ, ρ). It will have degenerated into a straight line...

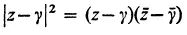
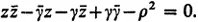
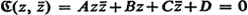
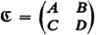
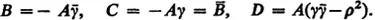
Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• Dedication
• Preface
• Introduction
• Chapter I. Analytic Geometry Of Circles
• Chapter II. The Moebius Transformation
• Chapter III. Two-Dimensional Non-Euclidean Geometries
• Appendices
• Bibliography
• Supplementary Bibliography
• Index