Calculus of Variations

I. M. Gelfand, S. V. Fomin, S. V. Fomin

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486414485
• eBook ISBN: 9780486135014
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

Based on a series of lectures given by I. M. Gelfand at Moscow State University, this book actually goes considerably beyond the material presented in the lectures. The aim is to give a treatment of the elements of the calculus of variations in a form both easily understandable and sufficiently modern. Considerable attention is devoted to physical applications of variational methods, e.g., canonical equations, variational principles of mechanics, and conservation laws.
The reader who merely wishes to become familiar with the most basic concepts and methods of the calculus of variations need only study the first chapter. Students wishing a more extensive treatment, however, will find the first six chapters comprise a complete university-level course in the subject, including the theory of fields and sufficient conditions for weak and strong extrema. Chapter 7 considers the application of variational methods to the study of systems with infinite degrees of freedom, and Chapter 8 deals with direct methods in the calculus of variations. The problems following each chapter were made specially for this English-language edition, and many of them comment further on corresponding parts of the text. Two appendices and suggestions for supplementary reading round out the text.
Substantially revised and corrected by the translator, this inexpensive new edition will be welcomed by advanced undergraduate and graduate students of mathematics and physics.

1

ELEMENTS
OF THE THEORY

1. Functionals. Some Simple Variational Problems

Variable quantities called functionals play an important role in many problems arising in analysis, mechanics, geometry, etc. By a functional, we mean a correspondence which assigns a definite (real) number to each function (or curve) belonging to some class. Thus, one might say that a functional is a kind of function, where the independent variable is itself a function (or curve). The following are examples of functionals:

1. Consider the set of all rectifiable plane curves.¹ A definite number is associated with each such curve, namely, its length. Thus, the length of a curve is a functional defined on the set of rectifiable curves.

2. Suppose that each rectifiable plane curve is regarded as being made out of some homogeneous material. Then if we associate with each such curve the ordinate of its center of mass, we again obtain a functional.

3. Consider all possible paths joining two given points A and B in the plane. Suppose that a particle can move along any of these paths, and let the particle have a definite velocity v(x, y) at the point (x, y). Then we obtain a functional by associating with each path the time the particle takes to traverse the path.

4. Let y(x) be an arbitrary continuously differentiable function, defined on the interval [a, b].² Then the formula

defines a functional on the set of all such functions y(x).

5. As a more general example, let F(x, y, z) be a continuous function of three variables. Then the expression

where y(x) ranges over the set of all continuously differentiable functions defined on the interval [a, b], defines a functional. By choosing different functions F(x, y, z), we obtain different functionals. For example, if

J[y] is the length of the curve y = y(x), as in the first example, while if

F(x, y, z) = Z²,

J[y] reduces to the case considered in the fourth example. In what follows, we shall be concerned mainly with functionals of the form (1).

Particular instances of problems involving the concept of a functional were considered more than three hundred years ago, and in fact, the first important re...

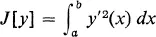
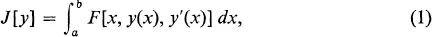
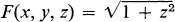
Table of contents

• Cover
• Title Page
• Copyright Page
• Authors’ Preface
• Translator’s Preface
• Table of Contents
• 1 Elements of the Theory
• 2 Further Generalizations
• 3 The General Variation of a Functional
• 4 The Canonical form of the Euler Equations and Related Topics
• 5 The second Variation. Sufficient Conditions for a weak Extremum
• 6 Fields. Sufficient Conditions for a Strong Extremum
• 7 Variational Problems Involving Multiple Integrals
• 8 Direct Methods in the Calculus of Variations
• Appendix I Propagation of Disturbances and the Canonical Equations
• Appendix II Variational methods in Problems of optimal control
• Bibliography
• Index