General Chemistry

Linus Pauling

• Publisher: Dover Publications
• Year: 2014
• ISBN:
  9780486134659
• Topic: Naturwissenschaften
• Subtopic: Chemie

`An excellent text, highly recommended.` — Choice
When it was first published, this first-year chemistry text revolutionized the teaching of chemistry by presenting it in terms of unifying principles instead of as a body of unrelated facts. Those principles included modern theories of atomic and molecular structure, quantum mechanics, statistical mechanics and thermodynamics. In addition, Dr. Pauling attempted to correlate the theories with descriptive chemistry, the observed properties of substances, to introduce the student to the multitude of chemical substances and their properties.
In this extensively revised and updated third edition, the Nobel Prize–winning author maintains an excellent balance between theoretical and descriptive material, although the amount of descriptive chemistry has been decreased somewhat, and the presentation of the subject, especially in relation to the nonmetals, has been revised in such a way as to permit greater correlation with the electronic structure of atoms, especially electronegativity.
The principles of quantum mechanics are discussed on the basis of the de Broglie wavelength of the electron. The quantized energy levels of a particle in a box are derived by means of a simple assumption about the relation of the de Broglie waves to the walls of the box. No attempt is made to solve the Schrodinger wave equation for other systems, but the wave functions of hydrogen-like electrons are presented and discussed in some detail, and the quantum states for other systems are also covered. Statistical mechanics is introduced before thermodynamics, and the discussion of thermodynamics is based on it. This arrangement reflects the author's belief that beginning students can understand statistical mechanics better than chemical thermodynamics.
Aimed at first-year college students who plan to major in chemistry or closely related fields, the book is written in a logical, clear and understandable style. In addition, many excellent figures are included, along with numerous problems and 75 pages of appendixes covering such topics as symmetry of molecules and crystals, hybrid bond orbitals, and magnetic properties of substances.

1

The Nature and Properties of Matter

1-1. Matter and Chemistry

The universe is composed of matter and radiant energy. Matter (from the Latin materia, meaning wood or other material) may be defined as any kind of mass-energy (see Section 1-2) that moves with velocities less than the velocity of light, and radiant energy as any kind of mass-energy that moves with the velocity of light.

The different kinds of matter are called substances. Chemistry is the science of substances—their structure, their properties, and the reactions that change them into other substances.

This definition of chemistry is both too narrow and too broad. It is too narrow because the chemist in his study of substances must also study radiant energy, in its interaction with substances. He may be interested in the color of substances, which is produced by the absorption of light. Or he may be interested in the atomic structure of substances, as determined by the diffraction of x-rays (Section 3-7 and Appendix IV) or by the absorption or emission of radiowaves by the substances.

On the other hand, the definition is too broad, in that almost all of science could be included within it. The astrophysicist is interested in the substances that are present in stars and other celestial bodies, or that are distributed, in very low concentration, through interstellar space. The nuclear physicist studies the substances that constitute the nuclei of atoms. The biologist is interested in the substances that are present in living organisms. The geologist is interested in the substances, called minerals, that make up the earth. It is hard to draw a line between chemistry and other sciences.

1-2. Mass and Energy

Matter has mass, and any portion of matter on the earth is attracted toward the center of the earth by the force of gravity; this attraction is called the weight of the portion of matter. For many years scientists thought that matter and radiant energy could be distinguished through the possession of mass by matter and the lack of possession of mass by energy. Then, early in the present century (1905), it was pointed out by Albert Einstein (1879-1955) that energy also has mass, and that light is accordingly attracted by matter through gravitation. This was verified by astronomers, who found that a ray of light traveling from a distant star to the earth and passing close by the sun is bent toward the sun by its gravitational attraction. The observation of this phenomenon was made during a solar eclipse, when the image of the star could be seen close to the sun.

The amount of mass associated with a definite amount of energy is given by an important equation, the Einstein equation, which is an essential part of the theory of relativity:

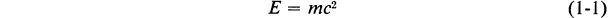
In this equation E is the amount of energy (J), m is the mass (kg), and c is the velocity of light (m s⁻¹).* The velocity of light, c, is one of the fundamental constants of nature;† its value is 2.9979 × 10⁸ meters per second.

Until the present century it was also thought that matter could not be created or destroyed, but could only be converted from one form into another. In recent years it has, however, been found possible to convert matter into radiant energy, and to convert radiant energy into matter. The mass m of the matter obtained by the conversion of an amount E of radiant energy or convertible into this amount of radiant energy is given by the Einstein equation. Experimental verification of the Einstein equation has been obtained by the study of processes involving nuclei of atoms. The nature of these processes will be described in later chapters in this book.

Until early in the present century scientists made use of a law of conservation of matter and a law of conservation of energy. These two conservation laws were then combined into a single one, the law of conservation of mass, in which the mass to be conserved includes both the mass of the matter in the system and the mass of the radiant energy in the system.

1-3. The International System of Units

The metric system of units of length, mass, force, and other physical quantities was developed during the French Revolution. Because of their greater convenience and simplicity, metric units have replaced native units (such as the foot and the pound) in scientific work everywhere and have been formally accepted for practical use in many countries (all except the United States, Canada, and some African countries). An extended and improved form of the metric system, called the International System (IS, or sometimes SI, for Systéme International), was formally adopted by the General Conference of Weights and Measures in 1960.

The symbols of the basic IS units and of the prefixes for fractions and multiples and those for some derived IS units are given in Appendix I. If you have made use of the MKS system (meter-kilogram-second system) in your study of physics the IS system will be familiar to you, for the most part, but if you have made use of the cgs system (centimeter-gram-second system) you will have to learn some new units.

The IS unit of mass, the kilogram, is defined as the mass of a standard object made of a platinum-iridium alloy and kept in Paris. One pound is equal approximately to 453.59 g, and hence 1 kg is equal approximately to 2.205 lb. (Note that it has become customary for the abbreviation of units in the metric system to be written without periods.) There is at the present time a flaw in the International System, in that the name for the unit of mass involves a prefix, kilo. This flaw will remain until agreement about a new name and symbol has been reached. In the meantime we must remember that 1 milligram (symbol 1 mg, not 1 μkg) is one millionth of the unit of mass, not one thousandth, as indicated by the prefix milli.

The IS unit of length, the meter (m), is equal to about 39.37 inches (1 inch equals exactly 2.54 cm). The meter was formerly defined as the distance between two engraved lines on a standard platinum-iridium bar kept in Paris by the International Bureau of Weights and Measures; in 1960 it was redefined, by international agreement, as 1,650,763.73 wavelengths of the orange-red spectral line* of krypton 86.

The IS unit of time is the second (s). It is defined as the interval occupied by 9,192,631,770 cycles of the microwave line* of cesium 133 with wavelength about 3.26 cm. The second was formerly defined as 1/86400th of the mean solar day.

The IS unit of volume is the cubic meter, m³. In chemistry a unit that is much used† is the liter, symbol 1, which is 1 × 10⁻³ m³. The milliliter, 1 × 10⁻³ 1, is equal to the cubic centimeter: 1 ml = 1 cm³.

The IS unit of force is the newton (N), which is defined as the force needed to accelerate a mass of 1 kg by 1 m s⁻². The newton is 10⁵ dyne (the dyne, the unit of force in the cgs system, is the force that accelerates 1 g by 1 cm s⁻²). The IS unit of energy, the joule‡ (J), is the work done by 1 newton in the distance 1 meter: 1 J = 1 N m = 10⁷ erg = 10⁷ dyne cm.

In chemistry the calorie has been extensively used as the unit of energy. The thermochemical calorie, defined as 4.184 J (Appendix I), is approximately the amount of energy needed to raise the temperature of 1 g of water by 1°C. The large calorie (kcal or Cal) is 10³ cal. In this book we shall use the joule in most of the tables and discussions. Since most thermochemical reference books use the calorie or kilocalorie, you will find it worth while to remember the conversion factor:

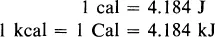
Example 1-1. Niagara Falls (Horseshoe) is 160 feet high. How much warmer is the water at the bottom than at the top, as the result of the conversion of potential energy into thermal energy? The standard acceleration of gravity is 9.80665 m s⁻².

Solution. The gravitational force on a mass of 1 kg at the earth’s surface is 9.80665 N. The change is potential energy of 1 kg over a vertical distance h (in meters) is 9.80665 × h J. In this problem h has the value 0.3048 × 160 = 48.77 m (conversion factor from Appendix I); hence the change in potential energy produces 9.80665 × 48.77 = 478 J of thermal energy. The energy required to raise the temperature of 1 kg of water by 1°C is given above as 1 kcal = 4.184 kJ = 4184 J. Hence the increase in temperature of the water is 478/4184 = 0.114°C.

Example 1-2.When 2 kg of uranium 235 undergoes nuclear fission (as in the detonation of the Hiroshima atomic bomb on 6 August 1945), 1.646 × 10¹⁴ J of radiant energy and thermal energy is liberated. What is the mass of the material products of the reaction?

Solution. We can calculate the mass of the liberated energy by the use of the Einstein equation (1-1). Rewriting this equation by dividing each side by c² and introducing the values of E and c, we obtain

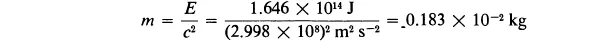
Thus, the material mass of 2 kg has decreased by 0.00183 kg (that is, by 0.0915%), leaving material products of the reaction with mass 1.99817 kg.

The Einstein relation between mass and energy has been verified by the direct measurement of the mass of the products and of the energy emitted in nuclear reactions.

Example 1-3. It is found by experiment that when 1 kg of glyceryl trinitrate (nitroglycerine) is exploded, the amount 8.0 × 10⁶ J of energy is liberated. What is the mass of the products of the explosion?

Solution. This example is to be solved in exactly the same way as the preceding one. The mass of the radiant energy that is produced by the explosion is obtained by dividing the energy, E, by the square of the velocity of light:

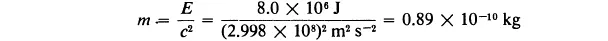
Thus we calculate that the mass of the products of the explosion is 0.999999999911 kg.

We see that the mass of the products of this chemical reaction differs very slightly from the mass of the reactant—so slightly that it is impossible to detect the change in a direct way. The change, less than one part in ten billion (1 in 10¹⁰), is so small that for practical purposes we may say that there is conservation of mass in ordinary chemical reactions.

1-4. Temperature

If two objects are placed in contact with one another, thermal energy may flow from one object to the other one. Temperature is the quality that determines the direction in which thermal energy flows—it flows from the object at higher temperature to the object at lower temperature.

Temperatures are ordinarily measured by means of a thermometer, such as the ordina...

Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• 1 The Nature and Properties of Matter
• 2 The Atomic and Molecular Structure of Matter
• 3 The Electron, the Nuclei of Atoms, and the Photon
• 4 Elements and Compounds. Atomic and Molecular Masses
• 5 Atomic Structure and the Periodic Table of the Elements
• 6 The Chemical Bond
• 7 The Nonmetallic Elements and Some of Their Compounds
• 8 Oxygen Compounds of Nonmetallic Elements
• 9 Gases: Quantum Mechanics and Statistical Mechanics
• 10 Chemical Thermodynamics
• 11 Chemical Equilibrium
• 12 Water
• 13 The Properties of Solutions
• 14 Acids and Bases
• 15 Oxidation-Reduction Reactions. Electrolysis
• 16 The Rate of Chemical Reactions
• 17 The Nature of Metals and Alloys
• 18 Lithium, Beryllium, Boron, and Silicon and Their Congeners
• 19 Inorganic Complexes and the Chemistry of the Transition Metals
• 20 Iron, Cobalt, Nickel, and the Platinum Metals
• 21 Copper, Zinc, and Gallium and Their Congeners
• 22 Titanium, Vanadium, Chromium, and Manganese and Their Congeners
• 23 Organic Chemistry
• 24 Biochemistry
• 25 The Chemistry of the Fundamental Particles
• 26 Nuclear Chemistry
• Appendixes
• Index