Theory of Flight

Richard von Mises

• Publisher: Dover Publications
• Year: 2012
• eBook ISBN: 9780486132228
• Topic: Technology & Engineering
• Subtopic: Aeronautic & Astronautic Engineering
• Index: Technology & Engineering

"An outstanding textbook." — Scientific, Medical and Technical Books
Almost unsurpassed as a balanced, well-written account of fundamental fluid dynamics, Theory of Flight may still be recommended for a clearer presentation than is to be forced in many more recent works, though it is limited to situations in which air compressibility effects are unimportant.
Designed for the college senior or beginning graduate student, the text assumes a knowledge of the principles of calculus and some training in general mechanics. It is unusual in offering a well-balanced introduction, stressing equally theory and practice. It avoids the formidable mathematical structure of fluid dynamics, while conveying by often unorthodox methods a full understanding of the physical phenomena and mathematical concepts of aeronautical engineering. Theory of Flight contains perhaps the best introduction to the general theory of stability, while the introduction to dynamics of incompressible fluids and the chapters on wing theory remain particularly valuable for their clarity of exposition and originality of thought.
Mises' position as one of the great pioneers in the development of the aeronautical sciences lends a flavor of authenticity not found in more conventional textbooks. Any student who has made himself familiar with his exposition of the fundamentals and applications will have acquired an excellent background for additional, more specialized fields of modern aeronautical engineering.

Part One

EQUILIBRIUM AND STEADY FLOW IN THE ATMOSPHERE

CHAPTER I

THE ATMOSPHERE AT REST

1. Density. Pressure. Equation of State.

In kinetic theory a gas is considered as composed of discrete molecules in vigorous, irregular motion, continually colliding with one another. In fluid dynamics one substitutes for this picture the simpler one of continuously distributed matter moving without sudden changes of velocity.

At any point P of a region in space occupied by such a continuous medium, or continuum, the density can be defined in the following way: Consider the mass and the volume of the substance that is contained in a small region R surrounding the point P. The density at P then is the limiting value of the ratio of the mass to the volume as the linear dimensions of R tend simultaneously to zero.

In this book the density will be denoted by ρ. In the engineering system the unit of density is one slug per cubic foot. At 59°F. and standard atmospheric pressure (29.921 in. Hg) the density of dry air is 0.002378 slug/ft.³

The specific weight γ, defined as the weight per unit of volume, is the product of the density and the acceleration g of free fall: γ = gρ. In the engineering system the unit of specific weight is the pound per cubic foot. With g = 32.174 ft./sec.², the specific weight of dry air at 59°F. and standard pressure is seen to be 0.07651 lb./ft.³

Consider two portions C₁ and C₂ of the continuum touching each other at the point P. Around P mark off an infinitesimal area dS (Fig. 1). Across dS the portion C₂ exerts an infinitesimal force on the portion C₁. Denote the magnitude of this force by dF. The stress that C₂ exerts at P across the surface S on the portion C₁ of the continuum then is defined as the vector whose magnitude is dF/dS and whose direction is that of the infinitesimal force dF. It follows from Newton’s third law of motion that the stress which C₁ exerts at P across the surface S on the portion C₂ is given by a vector of the same magnitude and the opposite direction.

It is a fundamental assumption of the mechanics of continua that the stress transmitted at P across dS will not depend on the shape of the surfaces S₁ and S₂ as long as the tangential plane of both surfaces at P remains the same. We thus can speak of the stress transmitted across a surface element without defining the surfaces to which this element belongs and the portions C₁ and C₂ which they confine.

The stress transmitted across a surface element is in general oblique to it. The stress components perpendicular and parallel to the surface element are called normal stress and shearing stress, respectively. The normal stress can be a thrust or a tension.

FIG. 1.

In this book the continuum to be considered is the atmospheric air. Its mechanical properties are essentially the same as those of other gases and partly the same as those of liquids. The word “fluid” will be used to designate both gases and liquids. It is assumed as the characteristic property of fluids that in a state of rest no shearing stresses are transmitted and that the normal stress on any surface element is a thrust. Moreover, this assumption is maintained in most problems of fluid in motion. If we do this we call the fluid a perfect fluid (see Sec. II.2).

By considering a small portion of fluid enclosing a point P we can prove that the normal stress has the same value for any surface element through P if no shearing stress exists. Take a small tetrahedron PQ_xQ_yQ_z, three edges of which are parallel to the axes of a system of rectangular coordinates (Fig. 2). Let dS be the area of the face Q_xQ_yQ_z oblique to these edges and α its angle with the y-z-plane. Then dS_x = dS cos α is the area of the face parallel to the y-z-plane. Denote the normal stresses transmitted across the faces dS_x and dS by p_x and p, respectively. The force exerted by the fluid outside the tetrahedron on the face dS_x has the direction of the x-axis and the intensity p_x dS_x. The force p dS acting on the face dS is perpendicular to this face and thus makes the angle α with the x-axis. The forces acting on the two remaining faces are perpendicular to the x-axis. Thus the sum of the x-components of the forces acting on the portion of fluid under consideration is

p_x dS_x − p dS cos α = (p_x − p) dS_x

because dS_x = dS cos α. According to Newton’s second law this sum must equal the product of mass times acceleration component a_x in the x-direction. The mass is the product of the density ρ and the volume, which is

. Therefore,

FIG. 2.

To secure a finite value of a_x we have to assume that p_x − p tends toward zero if

becomes smaller and smaller, i.e., if the tetrahedron reduces to the point P. Thus the two stresses p_x and p on the two surface elements in P must be equal. Since the direction of the x-axis can be chosen arbitrarily, there exists only one stress value in P, or the state of stress at any point P of a perfect fluid, or of any fluid in equilibrium, is completely specifie...

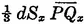
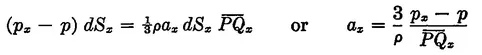
Table of contents

• DOVER BOOKS ON PHYSICS
• Title Page
• Copyright Page
• Dedication
• INTRODUCTION TO DOVER EDITION
• PREFACE
• Table of Contents
• Part One - EQUILIBRIUM AND STEADY FLOW IN THE ATMOSPHERE
• Part Two - THE AIRPLANE WING
• Part Three - PROPELLER AND ENGINE
• Part Four - AIRPLANE PERFORMANCE
• Part Five - AIRPLANE CONTROL AND STABILITY
• BIBLIOGRAPHICAL AND HISTORICAL NOTES
• INDEX